TEA系列概述
TEA系列概述:
TEA算法是由剑桥大学计算机实验室的 David Wheeler 和 Roger Needham于1994年发明,TEA 是Tiny Encryption Algorithm的缩写,以加密解密速度快,实现简单著称。
TEA 算法每一次可以操作 64bit(8byte),采用 128bit(16byte) 作为 key,算法采用迭代的形式,推荐的迭代轮数是 64轮,最少 32 轮。
为解决 TEA 算法密钥表攻击的问题,TEA 算法先后经历了几次改进,从 XTEA 到 BLOCK TEA,直至最新的XXTEA。
XTEA 也称做 TEAN:
它使用与 TEA 相同的简单运算,但四个子密钥采取不正规的方式进行混合以阻止密钥表攻击。
Block TEA 算法可以对 32 位的任意整数倍长度的变量块进行加解密的操作:
该算法将 XTEA 轮循函数依次应用于块中的每个字,并且将它附加于被应用字的邻字。
XXTEA使用跟Block TEA相似的结构:
但在处理块中每个字时利用了相邻字,且用拥有两个输入量的 MX 函数代替了 XTEA 轮循函数。
上面提到的相邻字其实就是数组中相邻的项。
TEA 系列算法中均使用了一个 DELTA 常数,但 DELTA 的值对算法并无什么影响,只是为了避免不良的取值,推荐DELTA 的值取为黄金分割数 (5√-2)/2 与 232 的乘积,取整后的十六进制值为 0x9e3779B9,用于保证每一轮加密都不相同。
TEA加密
介绍
TEA 采用与 DES 算法类似的 Feistel 结构,迭代的每次循环使用加法和移位操作,对明文和密钥进行扩散和混乱,实现明文的非线性变换。TEA 密钥长度和迭代次数都是 DES 的两倍,抗“试错法”攻击的强度不低于 DES 算法。算法以32bits 的字为运算单位,而不是耗费计算能力的逐位运算。算法没有采用 DES 那样的转换矩阵,它安全、高效、占用存储空间少,非常适合在嵌入式系统中应用
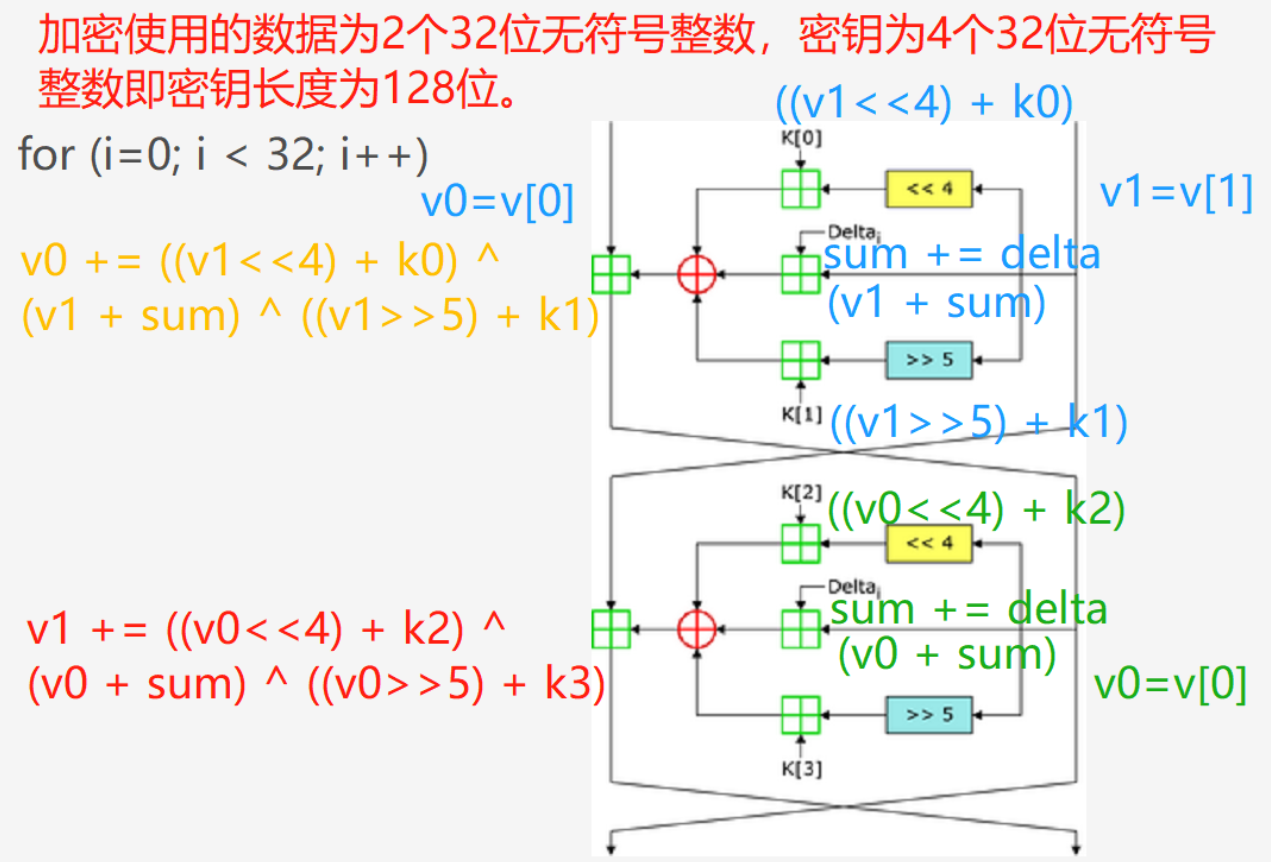
实现
C语言版
#include <stdio.h>
#include <stdint.h>
void encrypt (uint32_t *v,uint32_t *k)
{
uint32_t v0=v[0],v1=v[1],sum=0,i; //初始化变量 v0v1分别取输入数据的两个部分
uint32_t delta=0x9e3779b9;
uint32_t k0=k[0],k1=k[1],k2=k[2],k3=k[3]; //从密钥中取出四个部分
for(i=0;i<32;i++)
{
sum+=delta;
v0+=((v1<<4)+k0)^(v1+sum)^((v1>>5)+k1);
v1+=((v0<<4)+k2)^(v0+sum)^((v0>>5)+k3);
}
v[0]=v0;
v[1]=v1;
}
void decrypt(uint32_t *v,uint32_t *k)
{
uint32_t v0=v[0],v1=v[1],sum=0xc6ef3720,i; //sum是0x9e3778b9*32截取32位的结果
uint32_t delta=0x9e3779b9;
uint32_t k0=k[0],k1=k[1],k2=k[2],k3=k[3];
for(i=0;i<32;i++)
{
v1-=((v0<<4)+k2)^(v0+sum)^((v0>>5)+k3); //就是上面加密的过程逆过来
v0-=((v1<<4)+k0)^(v1+sum)^((v1>>5)+k1);
sum-=delta;
}
v[0]=v0;
v[1]=v1;
}
int main()
{
uint32_t v[2]={1,2},k[4]={2,2,3,4};
printf("加密前的数据:%u %u\n",v[0],v[1]);
encrypt(v,k);
printf("加密后数据:%u %u\n",v[0],v[1]);
decrypt(v,k);
printf("解密后数据:%u %u\n",v[0],v[1]);
}python版
from ctypes import *
def encrypt(v,k):
v0=c_uint32(v[0])
v1=c_uint32(v[1])
sum1=c_uint32(0)
delta=0x9e3779b9
for i in range(32):
sum1.value+=delta
v0.value+=((v1.value<<4)+k[0])^(v1.value+sum1.value)^((v1.value>>5)+k[1])
v1.value+=((v0.value<<4)+k[2])^(v0.value+sum1.value)^((v0.value>>5)+k[3])
return v0.value,v1.value
def decrypt(v,k):
v0=c_uint32(v[0])
v1=c_uint32(v[1])
delta=0x9e3779b9
sum1=c_uint32(delta*32)
for i in range(32):
v1.value-=((v0.value<<4)+k[2])^(v0.value+sum1.value)^((v0.value>>5)+k[3])
v0.value-=((v1.value<<4)+k[0])^(v1.value+sum1.value)^((v1.value>>5)+k[1])
sum1.value-=delta
return v0.value,v1.value
if __name__=='__main__':
a=[1,2]
k=[2,2,3,4]
print("加密前的数据",a)
res=encrypt(a,k)
print("加密后的数据:",res)
res=decrypt(res,k)
print("解密后的数据:",res)XTEA加密
介绍
XTEA是TEA的升级版:
增加了更多的密钥表,移位和异或操作等等
增加了爆破key的难度,但是加密解密的逻辑还是一样的
下图为流程图
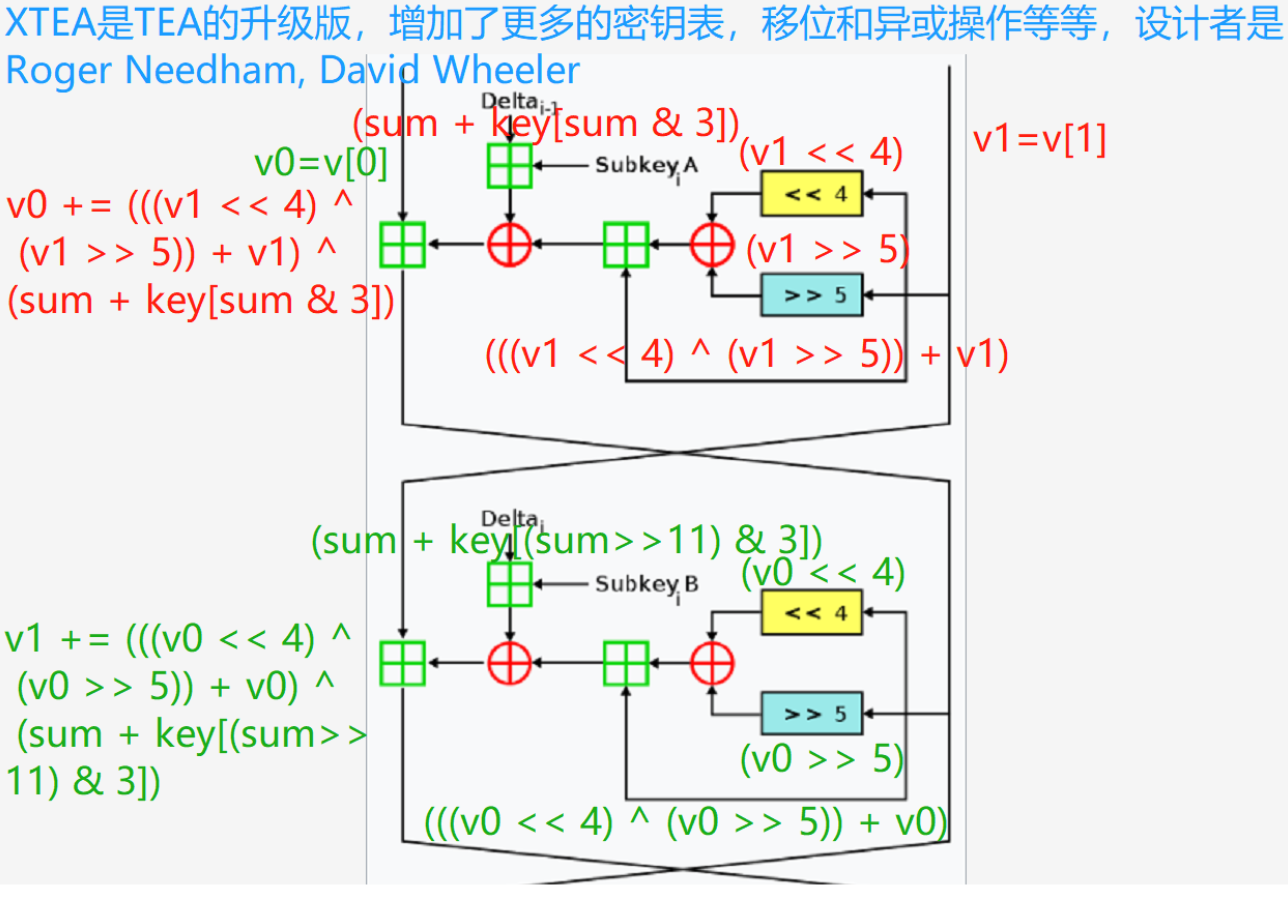
实现
C语言版
#include<stdio.h>
#include<stdint.h>
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]){
unsigned int i;
uint32_t v0=v[0],v1=v[1],sum=0,delta=0x9E3779B9;
for(i=0;i<num_rounds;i++){
v0+=(((v1<<4)^(v1>>5))+v1)^(sum+key[sum&3]);
sum+=delta;
v1+=(((v0<<4)^(v0>>5))+v0)^(sum+key[(sum>>11)&3]);
}
v[0]=v0;v[1]=v1;
}
void decipher(unsigned int num_rounds,uint32_t v[2],uint32_t const key[4]){
unsigned int i;
uint32_t v0=v[0],v1=v[1],delta=0x9E3779B9,sum=delta*num_rounds;
for(i=0;i<num_rounds;i++){
v1-=(((v0<<4)^(v0>>5))+v0)^(sum+key[(sum>>11)&3]);
sum-=delta;
v0-=(((v1<<4)^(v1>>5))+v1)^(sum+key[sum&3]);
}
v[0]=v0;v[1]=v1;
}
int main(){
uint32_t v[2]={1,2};
uint32_t const k[4]={2,2,3,4};
unsigned int r=32; //这里是加密轮数,自己设置
printf("加密前原始数据:%u %u\n",v[0],v[1]);
encipher(r,v,k);
printf("加密后原始数据:%u %u\n",v[0],v[1]);
decipher(r,v,k);
printf("解密后原始数据:%u %u\n",v[0],v[1]);
return 0;
}python版
from ctypes import *
def encrypt(v,k):
v0=c_uint32(v[0])
v1=c_uint32(v[1])
sum1=c_uint32(0)
delta=0x9e3779b9
for i in range(32):
v0.value+=(((v1.value<<4)^(v1.value>>5))+v1.value)^(sum1.value+k[sum1.value&3])
sum1.value+=delta
v1.value+=(((v0.value<<4)^(v0.value>>5))+v0.value)^(sum1.value+k[(sum1.value>>11)&3])
return v0.value,v1.value
def decrypt(v,k):
v0=c_uint32(v[0])
v1=c_uint32(v[1])
delta=0x9e3779b9
sum1=c_uint32(delta*32)
for i in range(32):
v1.value-=(((v0.value<<4)^(v0.value>>5))+v0.value)^(sum1.value+k[(sum1.value>>11)&3])
sum1.value-=delta
v0.value-=(((v1.value<<4)^(v1.value>>5))+v1.value)^(sum1.value+k[sum1.value&3])
return v0.value,v1.value
if __name__=='__main__':
a=[1,2]
k=[2,2,3,4]
print("加密前数据:",a)
res=encrypt(a,k)
print("加密后的数据:",res)
res=decrypt(res,k)
print("解密后数据:",res)XXTEA
介绍
XXTEA算法介绍:
XXTEA,又称Corrected Block TEA,是XTEA的升级版 ,设计者是Roger Needham, David Wheeler。
XXTEA是一个非平衡Feistel网络分组密码,在可变长度块上运行,这些块是32位大小的任意倍数(最小64位),使用128位密钥, 是目前TEA系列中最安全的算法,但性能较上两种有所降低。
算法流程如下
- 输入和密钥设置:
- 输入数据被分成32位无符号整数的块。
- 密钥通常由4个32位无符号整数组成。
- 数据块和密钥的选择取决于应用的具体需求。
- 轮迭代:
- XXTEA算法的加密和解密都采用迭代的方式,通常是32轮。
- 迭代中的基本操作是对两个32位无符号整数进行加密或解密。
- 加密过程:
- 对每一轮的迭代,先将待加密数据分成两个32位部分(通常称为v0和v1)。
- 使用轮密钥对数据进行操作。密钥也分为两个32位部分,通常称为k0和k1。
- 执行一系列位运算和加法运算,包括左移、右移、异或等。
- 对每轮迭代的结果进行累加。
- 解密过程:
- 解密过程与加密过程相反,同样进行32轮迭代。
- 对每一轮的迭代,使用轮密钥进行操作,执行一系列位运算和减法运算。
- 对每轮迭代的结果进行累减。
- 最后的结果:
- 经过32轮迭代后,得到加密或解密后的数据块。
图解为

实现
#include <stdio.h>
#include <stdint.h>
#define DELTA 0x933779b9
#define MX (((z>>5^y<<2)+(y>>3^z<<4))^((sum^y)+(key[(p&3)^e]^z)))
//MX是一个混淆运算宏
void btea(uint32_t *v,int n,uint32_t const key[4])
{
uint32_t y,z,sum;
unsigned p,rounds,e;
//加密算法
if(n>1)
{
rounds=6+52/n; //这个可以说是预定义值,n=2是rounds=32,n
sum=0; //n是多少就把密文分为n部分
z=v[n-1]; //z是待处理数据块的最后一个32位部分
do{
sum+=DELTA;
e=(sum>>2)&3; //e用于计算每轮的轮密钥
for(p=0;p<n-1;p++)
{
y=v[p+1];
z=v[p]+=MX;
}
y=v[0];
z=v[n-1]+=MX;
}
while(--rounds);
}
//解密算法
else if (n<-1)
{
n=-n;
rounds=6+52/n;
sum=rounds*DELTA;
y=v[0];
do
{
e=(sum>>2)&3;
for(p=n-1;p>0;p--)
{
z=v[p-1];
y=v[p]-=MX;
}
z=v[n-1];
y=v[0]-=MX;
sum-=DELTA;
}while(--rounds);
}
}
int main()
{
uint32_t v[2]={1,2};//密文
uint32_t const k[4]={2,2,3,4};
int n=2;
printf("加密前原始数据:%u %u\n",v[0],v[1]);
btea(v,n,k);
printf("加密后数据:%u %u\n",v[0],v[1]);
btea(v,-n,k);
printf("解密后数据:%u %u\n",v[0],v[1]);
}Python版本
from ctypes import *
def MX(z, y, sum1, k, p, e):
return c_uint32(((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[(p&3)^e.value]^z.value)))
def btea(v,k,n,delta):
if n>1:
sum1=c_uint32(0)
z=c_uint32(v[n-1])
rounds=6+52//n
e=c_uint32(0)
while rounds>0:
sum1.value+=delta
e.value=((sum1.value>>2)&3) #e都要32位哦
for p in range(n-1):
y=c_uint32(v[p+1])
#v[p]=c_uint32(v[p]+c_uint32((((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[(p&3)^e.value]^z.value)))).value).value
v[p] = c_uint32(v[p] + MX(z,y,sum1,k,p,e).value).value
z.value=v[p]
y=c_uint32(v[0])
#v[n-1]=c_uint32(v[n-1]+c_uint32((((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[((n-1)&3)^e.value]^z.value)))).value).value #这里tmd传入的是k[((n-1)&3)啊我草,找了半天!!!
v[n-1] = c_uint32(v[n-1] + MX(z,y,sum1,k,n-1,e).value).value
z.value=v[n-1]
rounds-=1
else:
sum1=c_uint32(0)
n=-n
rounds=6+52//n
sum1.value=rounds*delta
y=c_uint32(v[0])
e=c_uint32(0)
while rounds>0:
e.value=((sum1.value>>2)&3) #e都要32位哦
for p in range(n-1, 0, -1):
z=c_uint32(v[p-1])
#y[p]=c_uint32(v[p]-c_uint32((((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[(p&3)^e.value]^z.value)))).value).value
v[p] = c_uint32(v[p] - MX(z,y,sum1,k,p,e).value).value
y.value=v[p]
z=c_uint32(v[n-1])
#v[n-1]=c_uint32(v[n-1]-c_uint32((((z.value>>5^y.value<<2)+(y.value>>3^z.value<<4))^((sum1.value^y.value)+(k[((n-1)&3)^e.value]^z.value)))).value).value #这里tmd传入的是k[((n-1)&3)啊我草,找了半天!!!
v[0] = c_uint32(v[0] - MX(z,y,sum1,k,0,e).value).value
y.value=v[0]
sum1.value-=delta
rounds-=1
return v
if __name__=='__main__':
a=[1,2]
k=[2,2,3,4]
delta=0x9e3779b9
n=2
print("加密前数据:",a)
res=btea(a,k,n,delta)
print("加密后数据:",res)
res=btea(a,k,-n,delta)
print("解密后数据:",res)TEA算法在ida中的分析与识别
- 可能存在针对64bit以及128bit数字的操作(输入的message和key)
- 存在先位移,后异或的类似操作。比如((z >> 5 ^ x <<4) ^ (y << 4 & q >> 5))等混合变换
- 全部你一个复杂的混合变换的结构可能会叠加到另一个值上,两者相互叠加(Feistel结构)
- 获取密钥的时候,会使用某一个常量值作为下标 (key [ (sum >> 11) & 3])
- 一开始会在算法定义一个delta,并且不断参与算法,但是不会受到输入的影响。
源码在上面已经给出:
- Debug32位,Vs2022
//IDAmain函数
int __cdecl main_0(int argc, const char **argv, const char **envp)
{
int v4[6]; // [esp+DCh] [ebp-28h] BYREF
char v5[4]; // [esp+F4h] [ebp-10h] BYREF
int v6; // [esp+F8h] [ebp-Ch]
__CheckForDebuggerJustMyCode(&unk_41C028);
*(_DWORD *)v5 = 1;
v6 = 2;
v4[0] = 2;
v4[1] = 2;
v4[2] = 3;
v4[3] = 4;
sub_4110CD((char *)&byte_417B30, 1);
sub_411186(32, v5, v4);
sub_4110CD((char *)&byte_417B4C, v5[0]);
sub_4110FF(32, v5, v4);
sub_4110CD((char *)&byte_417B68, v5[0]);
return 0;
}- sub_4110CDprintf函数
- sub_411186为Tea_encrypt函数
- sub_4110FF为Tea_decrypt函数
sub_411186函数
// attributes: thunk
int __cdecl sub_411186(int a1, int a2, int a3)
{
return sub_4118D0(a1, a2, a3);
}
int __cdecl sub_4118D0(unsigned int a1, unsigned int *a2, int a3)
{
int result; // eax
unsigned int v4; // [esp+DCh] [ebp-2Ch]
unsigned int v5; // [esp+E8h] [ebp-20h]
unsigned int v6; // [esp+F4h] [ebp-14h]
unsigned int i; // [esp+100h] [ebp-8h]
__CheckForDebuggerJustMyCode(&unk_41C028);
v6 = *a2;
v5 = a2[1];
v4 = 0;
for ( i = 0; i < a1; ++i )
{
v6 += (*(_DWORD *)(a3 + 4 * (v4 & 3)) + v4) ^ (v5 + ((v5 >> 5) ^ (16 * v5)));
v4 -= 1640531527;
v5 += (*(_DWORD *)(a3 + 4 * ((v4 >> 11) & 3)) + v4) ^ (v6 + ((v6 >> 5) ^ (16 * v6)));
}
*a2 = v6;
result = 4;
a2[1] = v5;
return result;
}- 1640531527为我们xtea算法中的Delta常数
- xtea算法与tea算法不同的是xtea算法的核心算法是在于取轮密钥,而不是像tea算法中,通过常数影响轮密钥
- (v5 + ((v5 >> 5) ^ ( 16 * v5))) 等价于 (v1 + ((v1 >> 5) ^ (v1 << 4)))其他同理.
XXTEA算法:
- Debug32位,Vs2022
//main函数代码
int __cdecl main_0(int argc, const char **argv, const char **envp)
{
int v4[6]; // [esp+DCh] [ebp-28h] BYREF
char v5[4]; // [esp+F4h] [ebp-10h] BYREF
int v6; // [esp+F8h] [ebp-Ch]
__CheckForDebuggerJustMyCode(&unk_41C029);
*(_DWORD *)v5 = 1;
v6 = 2;
v4[0] = 2;
v4[1] = 2;
v4[2] = 3;
v4[3] = 4;
sub_4110CD((char *)&byte_417B30, 1);
sub_4111E0((int)v5, 2, (int)v4);
sub_4110CD((char *)&byte_417B4C, v5[0]);
sub_4111E0((int)v5, -2, (int)v4);
sub_4110CD((char *)&byte_417B68, v5[0]);
return 0;
}- sub_4110CD对应printf函数
- sub_4111E0对应的是Tea_encrypt和Tea_decrypt函数
sub_4111E0函数
// attributes: thunk
int __cdecl sub_4111E0(int a1, int a2, int a3)
{
return sub_411770(a1, a2, a3);
}
int __cdecl sub_411770(unsigned int *a1, int a2, int a3)
{
int result; // eax
unsigned int v4; // eax
int v5; // edx
unsigned int v6; // edx
unsigned int v7; // edx
unsigned int v8; // edx
int v9; // [esp+D4h] [ebp-44h]
int v10; // [esp+D4h] [ebp-44h]
int v11; // [esp+E0h] [ebp-38h]
int v12; // [esp+E0h] [ebp-38h]
unsigned int j; // [esp+ECh] [ebp-2Ch]
int i; // [esp+ECh] [ebp-2Ch]
unsigned int v15; // [esp+F8h] [ebp-20h]
unsigned int v16; // [esp+F8h] [ebp-20h]
unsigned int v17; // [esp+104h] [ebp-14h]
unsigned int v18; // [esp+110h] [ebp-8h]
int v19; // [esp+124h] [ebp+Ch]
result = __CheckForDebuggerJustMyCode(&unk_41C029);
if ( a2 <= 1 )
{
if ( a2 < -1 )
{
v19 = -a2;
v12 = 52 / v19 + 6;
v16 = -1640531527 << (52 / v19 + 6);
v18 = *a1;
do
{
v10 = (v16 >> 2) & 3;
for ( i = v19 - 1; i; --i )
{
v7 = a1[i]
- (((a1[i - 1] ^ *(_DWORD *)(a3 + 4 * (v10 ^ i & 3))) + (v18 ^ v16)) ^ (((16 * a1[i - 1]) ^ (v18 >> 3))
+ ((4 * v18) ^ (a1[i - 1] >> 5))));
a1[i] = v7;
v18 = v7;
}
v8 = *a1
- (((a1[v19 - 1] ^ *(_DWORD *)(a3 + 4 * v10)) + (v18 ^ v16)) ^ (((16 * a1[v19 - 1]) ^ (v18 >> 3))
+ ((4 * v18) ^ (a1[v19 - 1] >> 5))));
*a1 = v8;
v18 = v8;
v16 += 1640531527;
result = --v12;
}
while ( v12 );
}
}
else
{
v11 = 52 / a2 + 6;
v15 = 0;
v17 = a1[a2 - 1];
do
{
v15 -= 0x61C88647;
v9 = (v15 >> 2) & 3;
for ( j = 0; j < a2 - 1; ++j )
{
v4 = ((v17 ^ *(_DWORD *)(a3 + 4 * (v9 ^ j & 3))) + (a1[j + 1] ^ v15)) ^ (((16 * v17) ^ (a1[j + 1] >> 3))
+ ((4 * a1[j + 1]) ^ (v17 >> 5)));
v5 = a1[j];
a1[j] = v4 + v5;
v17 = v4 + v5;
}
v6 = (((v17 ^ *(_DWORD *)(a3 + 4 * (v9 ^ j & 3))) + (*a1 ^ v15)) ^ (((16 * v17) ^ (*a1 >> 3))
+ ((4 * *a1) ^ (v17 >> 5))))
+ a1[a2 - 1];
a1[a2 - 1] = v6;
v17 = v6;
result = --v11;
}
while ( v11 );
}
return result;
}- 常量如果不确定的话,可以用IDA的插件findcrypt进行识别
- 见到移位+异或这种组合运算可以初步判断是tea系列算法
- 如果针对于每轮的轮数有不同的算法的话,可以确定是xxtea算法。