前言

​ 由于hust的sb课程设置，所以只有时间打第一周。快五一了终于有空闲时间了，把所有的reverse题目给复现一下

第一周

reverse

喵喵喵的flag碎了一地

​ 考点：ida的功能，没有值得学习的地方

聪明的信使

​ 考点：shift+f12 +凯撒加密

DebugMe

​ 考点：调试apk;jeb远程附加

android 调试基本原理

一般来说，Android 根据如下的顺序来判断一个应用是否可以被调试

  1. 检测 boot.img 中的 ro.debuggable 是否为 1，为 1 的话，手机中的任何应用均可以调试。
  2. 否则，检测对应应用中 AndroidManifest.xml 中 <application> 元素中是否包含了 android:debuggable=“true”，如果有的话，才会开启调试支持。

自然，我们也就有两种方法来使得一个应用可以被调试

  1. 将一个 apk 文件解包，在 <application> 元素中添加 android:debuggable=“true”，然后重打包，签名。
  2. 修改 boot.img 中的 ro.debuggable 为 1。

一般来说，因为前者需要我们每次都需要修改应用

ro.debuggable 的值可以根据如下命令来查询

adb shell getprop ro.debuggable

你是真的大学生吗？

考点：16位DOS下的汇编

enc = [0x76, 0x0e, 0x77, 0x14, 0x60, 0x06, 0x7d, 0x04, 0x6b, 0x1e,
       0x41, 0x2a, 0x44, 0x2b, 0x5c, 0x03, 0x3b, 0x0b, 0x33, 0x05]

dst = [0x00] * 20
for i in range(19):
    dst[i] = enc[i] ^ enc[i + 1]
dst[19] = enc[19] ^ enc[0]
print("".join([chr(i) for i in dst]))

Trustme

​ 非预期解：sql注入,万能密码直接出

​ 预期解：先用jadx看看mainactivity，解出一个提示，账号是admin；你看到的其实是假逻辑，真正的主函数被加固到dex里，可以从ProxyApplication中找到classes.dex的加密逻辑，即异或255然后写回apk;然后发现是从本地mydb.db中查询；直接拿到这个文件直接strings就能找到flag

baby unity

考点：il2cpp-unity逆向

利用il2cppdumper利用gm.dat把gameassembly.dll给dump出来；然后ida打开，恢复符号，利用cs文件找到函数的主逻辑，发现是个简单的异或

enc='XIcKYJU8Buh:UeV:BKN{U[JvUL??VuZ?CXJ;AX^{Ae]gA[]gUecb@K]ei^22'
enc_2=''
for i in enc:
    enc_2+=chr(ord(i)^0xF)
print(enc_2)
import base64
print(base64.b64decode(enc_2).decode('utf-8'))

misc

熊博士

atbash cipher

ez_隐写

伪加密，watermark，图片宽高爆破

有个压缩包，图片伪加密，先修复，把图片搞出来，然后修复宽高，得到提示：密码是开赛日

然后解压加密压缩包：名字是watermark，就是盲水印

利用吾爱破解论坛的watermark软件可以得到flag

game

谷歌识图

zzl的护理小课堂

F12查看源码，发现是本地验证

image-20240428195603099

有两种方式：

1.在这段代码前打个断点，然后控制台修改score=101

2.用burp改包，直接把服务端返回的 score改为101再返回本地浏览器

zip神之套

压缩包密码爆破，明文攻击

用ida打开给的exe文件，搜索字符串，给了个hint：密码是xyctf????????ftcyx

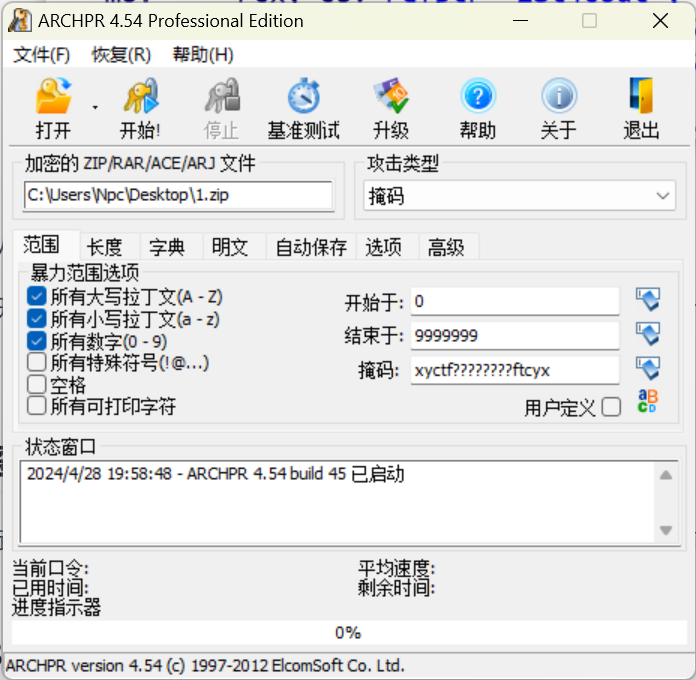
image-20240428195938482

用这种方式爆破

然后有两个zip，其中一个没加密，一个加密了，flag藏在加密的压缩包，然后ARPCH明文攻击

tcpl

risk-v架构程序，用qemu搭个riscv的虚拟机然后运行就可以出

网络迷踪

wireshark 跟踪tcp流量

随便翻翻，发现一段flag文本

随波逐流一把嗦 xxencode

XYCTF{fake_flag}
真正的flag格式：XYCTF{靶机ip地址_nmap扫描出的靶机开放的端口(由大到小排列 中间用_进行连接)_获
取靶机shell使用的漏洞的CVE编号}
例：XYCTF{1.1.1.1_888_88_8_CVE-2009-3103}

那就一步一步分析nmap的流量特征

回[SYN,ACK]的那三个TCP流量所展示的端口就是开放端口 135,139,445 然后因为是受害者回应攻击者，所以靶机IP为回应IP，即 192.168.204.133

CVE:SMB以及 IPC有关 的windows漏洞有关 直接搜索关键字 定位到 # Microsoft Windows Server - Code Execution (MS08-067)对应的CVE为CVE-2008-4250

crypto

factor

这道题目还是挺不错的，我当时卡了挺久，实际上你同构想一想把p3p^3当做p与q3q^3当做q就能利用wienerattack

import gmpy2
import hashlib
from Crypto.Util.number import *
import sympy as sp
# p = getPrime(512)
# q = getPrime(512)
# d = getPrime(512)
# e = gmpy2.invert(d, (p**3 - 1) * (q**3 - 1))

# print(e)
# print(p * q)
e=172005065945326769176157335849432320425605083524943730546805772515111751580759726759492349719668775270727323745284785341119685198468883978645793770975366048506237371435027612758232099414404389043740306443065413069994232238075194102578269859784981454218948784071599231415554297361219709787507633404217550013282713899284609273532223781487419770338416653260109238572639243087280632577902857385265070736208291583497988891353312351322545840742380550393294960815728021248513046077985900158814037534487146730483099151396746751774427787635287611736111679074330407715700153025952858666841328055071403960165321273972935204988906850585454805923440635864200149694398767776539993952528995717480620593326867245714074205285828967234591508039849777840636255379730281105670496110061909219669860172557450779495125345533232776767292561378244884362014224844319802810586344516400297830227894063759083198761120293919537342405893653545157892446163
pq=99075185389443078008327214328328747792385153883836599753096971412377366865826254033534293886034828804219037466246175526347014045811852531994537520303063113985486063022444972761276531422538694915030159420989401280012025249129111871649831185047820236417385693285461420040134313833571949090757635806658958193793
# x=sp.symbols('x')
# while True:
#     a=e//k*n
#     equation=sp.Eq(x**2+(n+1)*x+n**2-n+1-a,0)
#     solutions = sp.solveset(equation, x, domain=sp.Naturals)
#     if solutions:
#         print("解",solutions)
#         break
#     k+=1
import gmpy2
# numerator(n):分子, denominator(d)：分母
def t_cf(n, d):  # 将分数 x/y 转为连分数的形式
    res = []
    while d:
        res.append(n // d)
        n, d = d, n % d
    return res


def cf(sub_res):  # 得到渐进分数的分母和分子
    n, d = 1, 0
    for i in sub_res[::-1]:  # 从后面往前循环
        d, n = n, i * n + d
    return d, n


def list_fraction(x, y):  # 列出每个渐进分数
    res = t_cf(x, y)
    res = list(map(cf, (res[0:i] for i in range(1, len(res)))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def get_pq(a, b, c):  # 由p+q和pq的值通过维达定理来求解p和q(解二元一次方程)
    par = gmpy2.isqrt(b * b - 4 * a * c)  # 由上述可得，开根号一定是整数，因为有解
    x1, x2 = (-b + par) // (2 * a), (-b - par) // (2 * a)
    return x1, x2


def wienerAttack(e, n):
    for (d, k) in list_fraction(e, n):  # 用一个for循环来注意试探e/n的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if k == 0:  # 可能会出现连分数的第一个为0的情况，排除
            continue
        if (e * d - 1) % k != 0:  # ed=1 (mod φ(n)) 因此如果找到了d的话，(ed-1)会整除φ(n),也就是存在k使得(e*d-1)//k=φ(n)
            continue

        phi = (e * d - 1) // k  # 这个结果就是 φ(n)

        px, qy = get_pq(1, n - phi + 1, n)
        if px * qy == n:
            p, q = abs(int(px)), abs(int(qy))  # 可能会得到两个负数，负负得正未尝不会出现
            flag = "XYCTF{" + hashlib.md5(str(gmpy2.iroot(p,3)[0] + gmpy2.iroot(q,3)[0]).encode()).hexdigest() + "}"
            print(flag)
            d = gmpy2.invert(e, (p - 1) * (q - 1))  # 求ed=1 (mod  φ(n))的结果，也就是e关于 φ(n)的乘法逆元d
            print(p)
            print(q)
            return d
    print("求解d失败")

d=wienerAttack(e,pq**3)
print(d)
#flag = "XYCTF{" + hashlib.md5(str(p + q).encode()).hexdigest() + "}"

happy to solve1

异或的性质 p，q非常接近分解pq

from Crypto.Util.number import *
import sympy
import gmpy2
n=24852206647750545040640868093921252282805229864862413863025873203291042799096787789288461426555716785288286492530194901130042940279109598071958012303179823645151637759103558737126271435636657767272703908384802528366090871653024192321398785017073393201385586868836278447340624427705360349350604325533927890879
c=14767985399473111932544176852718061186100743117407141435994374261886396781040934632110608219482140465671269958180849886097491653105939368395716596413352563005027867546585191103214650790884720729601171517615620202183534021987618146862260558624458833387692782722514796407503120297235224234298891794056695442287
# # from secrets import flag
#
#
def get_happy_prime():
    p = getPrime(512)
    q = sympy.nextprime(p ^ ((1 << 512) - 1))
    return p, q
p,q=get_happy_prime()
print(p, '\n', q)
e = 65537
t1=1<<512
p = (2 ** 512 + gmpy2.iroot((2 ** 512) ** 2 - 4 * n, 2)[0]) // 2
p = int(p)
while n % p != 0:
    p = gmpy2.next_prime(p)
q = n // p
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

signin

from Crypto.Util.number import *
from tqdm import *
import gmpy2

flag = b'XYCTF{'
flag = bytes_to_long(flag)
leak = bin(int(flag))
#Padding 不足514位补0
while 1:
    leak += "0"
    if len(leak) == 514:
        break

#高位和低位交换位置
def swap_bits(input_str):
    input_list = list(input_str[2:])
    length = len(input_list)

    for i in range(length // 2):
        temp = input_list[i]
        input_list[i] = input_list[length - 1 - i]
        input_list[length - 1 - i] = temp

    return ''.join(input_list)


input_str = leak
result = swap_bits(input_str)
a = result


def custom_add(input_str):
    input_list = list(input_str)
    length = len(input_list)

    for i in range(length):
        input_list[i] = str((int(input_list[i]) + i + 1) % 10)

    result = ''.join(input_list)
    return result
def reverse_custom_add(result_str):
    input_list = list(result_str)
    length = len(input_list)

    for i in range(length):
        input_list[i] = str((int(input_list[i]) - i - 1) % 10)

    input_str = ''.join(input_list)
    return input_str


input_str = a
result = custom_add(input_str)
b = result
print(b)
b=12345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567890123456789012345678901234567891134567780012455678012234677801133467889112356678911245567891223457790013346788912235667801134456899122355788001235578891124566799013445778012235578800123467889112456678001245567991223557880012455788901334677800134456789122355788001235578890133566790013445778012235577900133467889112356678001245578801233467789112355779912234577990233556780113
re_b=reverse_custom_add(str(b))
print(re_b)
sp_re_b=swap_bits('0b'+re_b)
print(sp_re_b)
sp_re_b='1011000010110010100001101010100010001100111101101100010001100010011100100110101001110010011001100110100001101000010110100110000001100100110010000110110001011010011010001100010001110010011100000101101001110010011000100111001001101000010110100110110001101100011001100111001001101000011000001100100001100010011100101100110001110000110001001111101'
r_leak=int(sp_re_b,2)
print(r_leak)
print(long_to_bytes(r_leak))

BabyRSAMAX

题目：

from Crypto.Util.number import *
from gmpy2 import *
from random import choice

flag = b'XYCTF{******}'
e = '?'
def getBabyPrime(nbits):
    while True:
        p = 1
        while p.bit_length() <= nbits:
            p *= choice(sieve_base)
        
        if isPrime(p+1):
            return p+1

p = getBabyPrime(512)
q = getBabyPrime(512)
n = p*q
gift1 = (pow(p,e,n)-pow(q,e,n)) % n
gift2 = pow(p+q,e,n)

t = 65537
x = bytes_to_long(e)
y = pow(x, t, n)

m = bytes_to_long(flag)
c = powmod(m, e, n)

print(f'n = {n}')
print(f'gift1 = {gift1}')
print(f'gift2 = {gift2}')
print(f'c = {c}')
print(f'y = {y}')

'''
n = 39332423872740210783246069030855946244104982381157166843977599780233911183158560901377359925435092326653303964261550158658551518626014048783435245471536959844874036516931542444719549997971482644905523459407775392702211086149279473784796202020281909706723380472571862792003687423791576530085747716706475220532321
gift1 = 4549402444746338327349007235818187793950285105091726167573552412678416759694660166956782755631447271662108564084382098562999950228708300902201571583419116299932264478381197034402338481872937576172197202519770782458343606060544694608852844228400457232100904217062914047342663534138668490328400022651816597367310
gift2 = 111061215998959709920736448050860427855012026815376672067601244053580566359594802604251992986382187891022583247997994146019970445247509119719411310760491983876636264003942870756402328634092146799825005835867245563420135253048223898334460067523975023732153230791136870324302259127159852763634051238811969161011462
c = 16938927825234407267026017561045490265698491840814929432152839745035946118743714566623315033802681009017695526374397370343984360997903165842591414203197184946588470355728984912522040744691974819630118163976259246941579063687857994193309554129816268931672391946592680578681270693589911021465752454315629283033043
y = 1813650001270967709841306491297716908969425248888510985109381881270362755031385564927869313112540534780853966341044526856705589020295048473305762088786992446350060024881117741041260391405962817182674421715239197211274668450947666394594121764333794138308442124114744892164155894256326961605137479286082964520217

'''

gift1=pe−qe(modn)gift2=(p+q)e(modn)gift1=p^e-q^e (mod n)\quad gift2=(p+q)^e(mod n)

由二项式定理

gift2=pe+qe(modn)gift2=p^e+q^e(modn)

则

gift1+gift2≡2pe(modn)gift2−gift1≡2qe(modn)gift1+gift2\equiv2p^e(mod n)\quad gift2-gift1\equiv2q^e(mod n)

那么

pe=gift1+gift22(modn)qe=gift2−gift12(modn)p^e=\frac {gift1+gift2}{2}(mod n)\quad q^e=\frac {gift2-gift1}{2}(mod n)

然后就没什么思路了

其实这个题跟第一个等式没什么关系

利用B光滑数算法可以求出p，q

 N = 
39332423872740210783246069030855946244104982381157166843977599780233911183158560901377359925435092326653303964261550158658551518626014048783435245471536959844874036516931542444719549997971482644905523459407775392702211086149279473784796202020281909706723380472571862792003687423791576530085747716706475220532321
 a=2
 n=2
 from gmpy2 import *
 while True:
 a = pow(a, n, N)
 res = gcd(a-1, N)
 if res != 1 and res != N:
 q = N // res
 print("n=",n)
 print("p=",res)
 print("q=",q)
 break
 n += 1
 '''
 n= 97241
 p= 
2364384004775215979229504451537962651990724045771831909531148051705228759045517
 80358338769440558816351105253794964040981919231484098097671084895302287425479
 q= 
1663537893730573521952685751683977503626438222012535089410528359454206249832164
 56266478176579651490080696973849607356408696043718492499993062863415424578199
 '''
t=65537
p=23643840047752159792295044515379626519907240457718319095311480517052287590455 1780358338769440558816351105253794964040981919231484098097671084895302287425479
 q=16635378937305735219526857516839775036264382220125350894105283594542062498321
 6456266478176579651490080696973849607356408696043718492499993062863415424578199
 N=39332423872740210783246069030855946244104982381157166843977599780233911183158
 5609013773599254350923266533039642615501586585515186260140487834352454715369598
 4487403651693154244471954999797148264490552345940777539270221108614927947378479
 6202020281909706723380472571862792003687423791576530085747716706475220532321
 y=18136500012709677098413064912977169089694252488885109851093818812703627550313
 8556492786931311254053478085396634104452685670558902029504847330576208878699244
 6350060024881117741041260391405962817182674421715239197211274668450947666394594
 121764333794138308442124114744892164155894256326961605137479286082964520217
 from gmpy2 import *
 from libnum import n2s
 phi = (p-1)*(q-1)
 d=invert(t,phi)
 print(n2s(int(pow(y,d,N))))

这个应该是非预期解

复现

Reverse

ezunity

​ 其实与babyunity思路一致：

这里有两种想法：一是修复gm.dat；二是利用il2cpp-bridge-frida进行hook

不会trace导致卡了，浪费很多时间

trace真是个好东西

先说思路一（修复gm.dat）：把第一排改成AF 1B B1 FA 1D 00 00 00 00 01 00 00，删几个字符，让后面接着C0 B2 然后把下面的内容对齐 直接dumper导入，导入成功！然后沿用babyunity的方法直接静态分析即可

再说思路二（用frida进行hook）

记frida-il2cpp-bridge的使用-CSDN博客

这个教程讲的比较浅，frida还是需要深入学习，确实hook很方便

搭好环境，写个脚本，跟踪这个程序

import "frida-il2cpp-bridge";

Il2Cpp.perform(() => {

    console.log("Unity version: " + Il2Cpp.unityVersion);
    let ass = Il2Cpp.domain.assembly("Assembly-CSharp");         
    Il2Cpp.trace(true).assemblies(ass).and().attach()
    // const Assembly = Il2Cpp.domain.assembly("Assembly-CSharp").image;
    const SystemString = Il2Cpp.corlib.class("System.String");
    Il2Cpp.trace(true).classes(SystemString) 
        .classes(SystemString)
        .and()
        .attach();

    // console.log("Assembly-CSharp: " + Assembly)
    // console.log("System.String: " + SystemString);
});

显然是AES加密

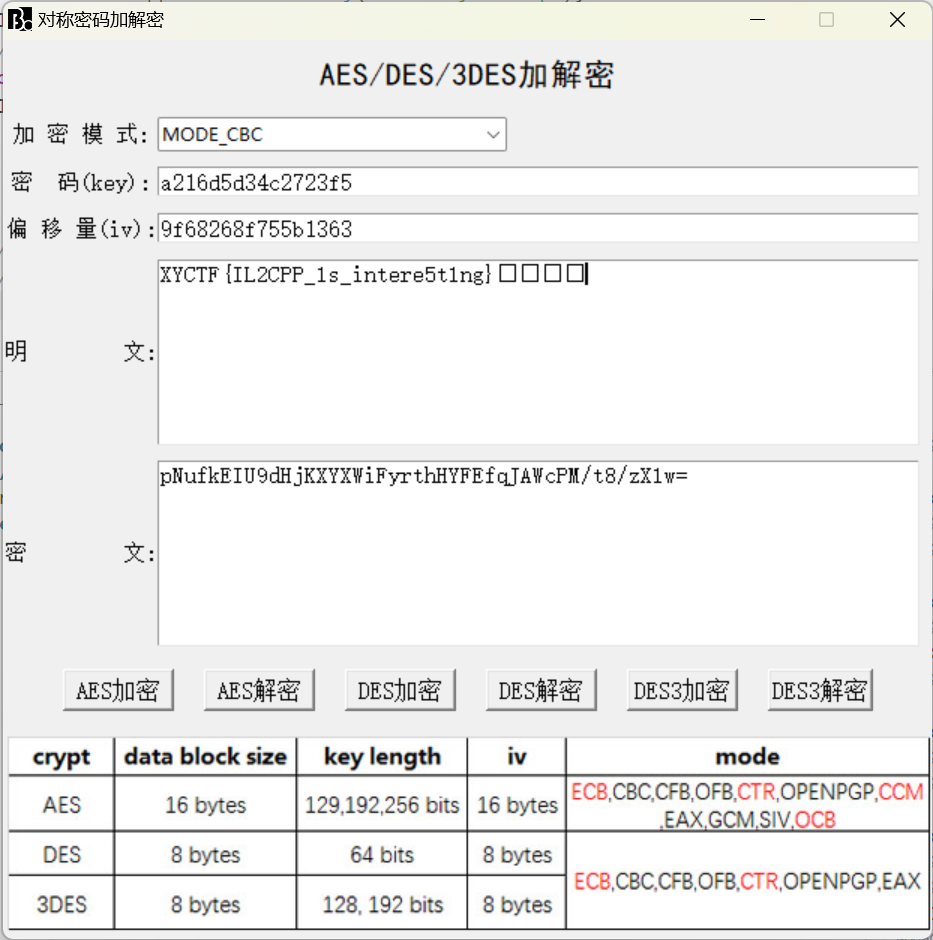
image-20240428223812164

e language

IDA7.5支持中文函数命名的办法 - 『逆向资源区』 - 吾爱破解 - LCG - LSG |安卓破解|病毒分析|www.52pojie.cn

fjqisba/E-Decompiler: 用来辅助分析易语言程序的IDA插件 (github.com)

image-20240429181425827

易语言逆向，又成脚本小子了 找到隐藏按钮的函数

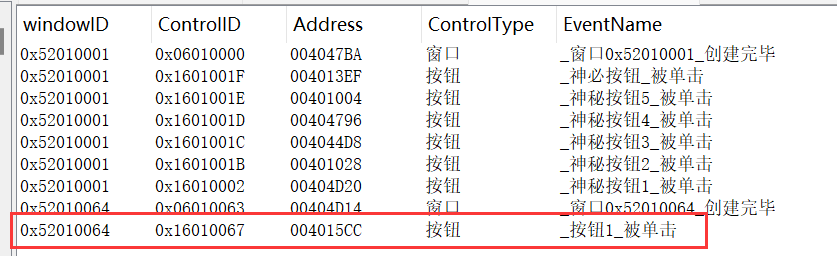
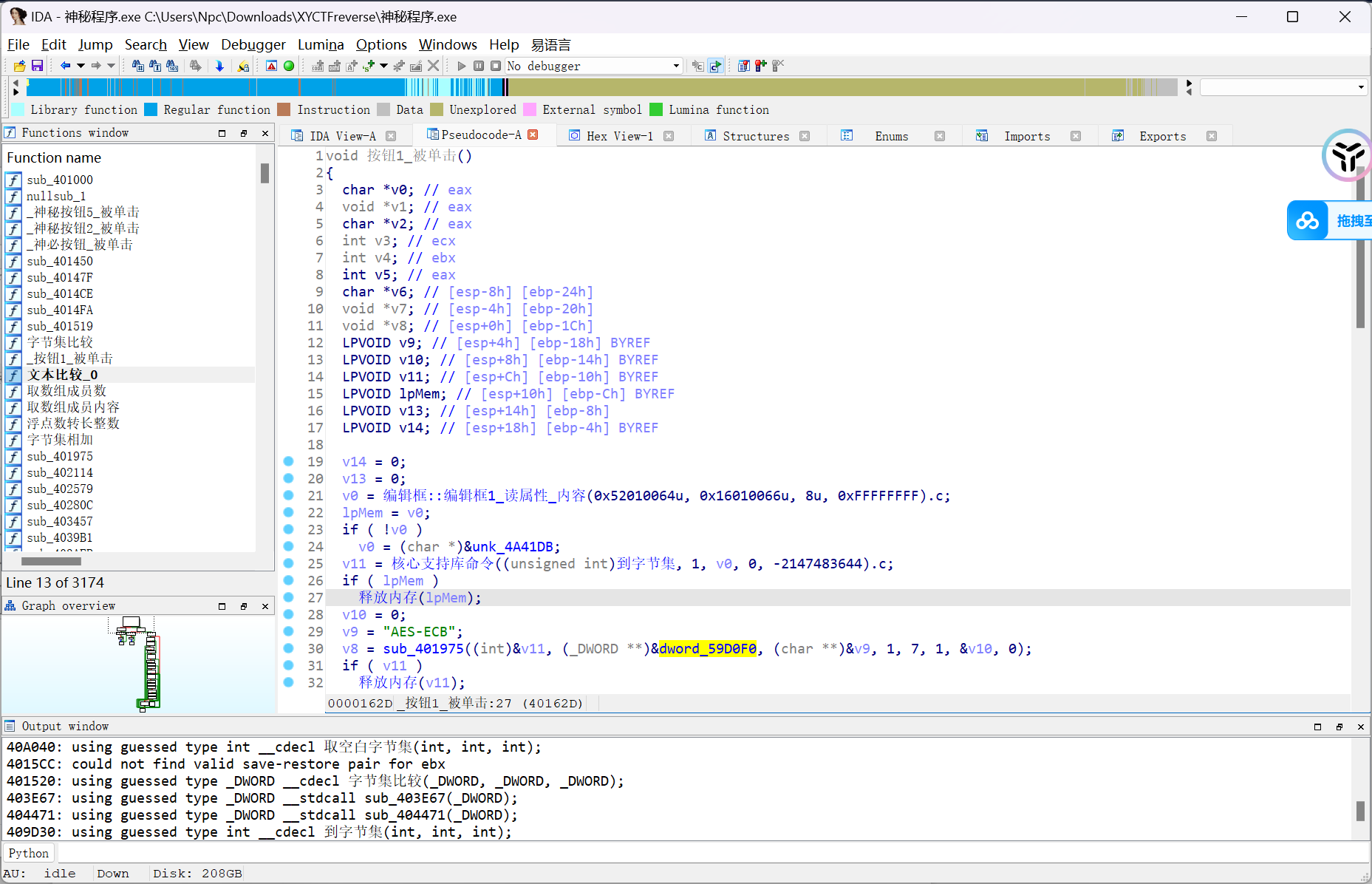
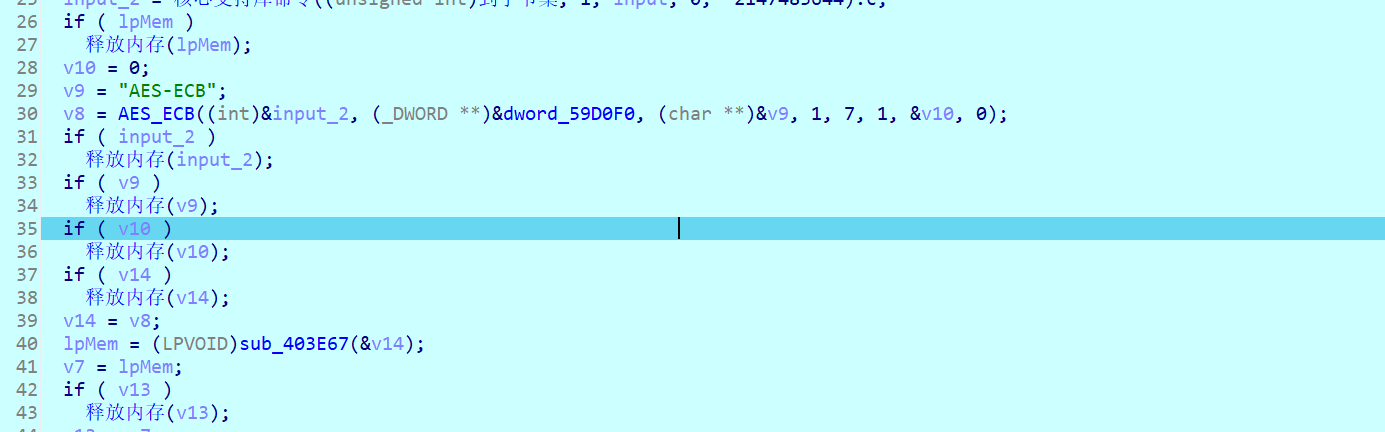
image-20240429181454271 image-20240429142439097 image-20240429143429187

动调提取key，再提密文

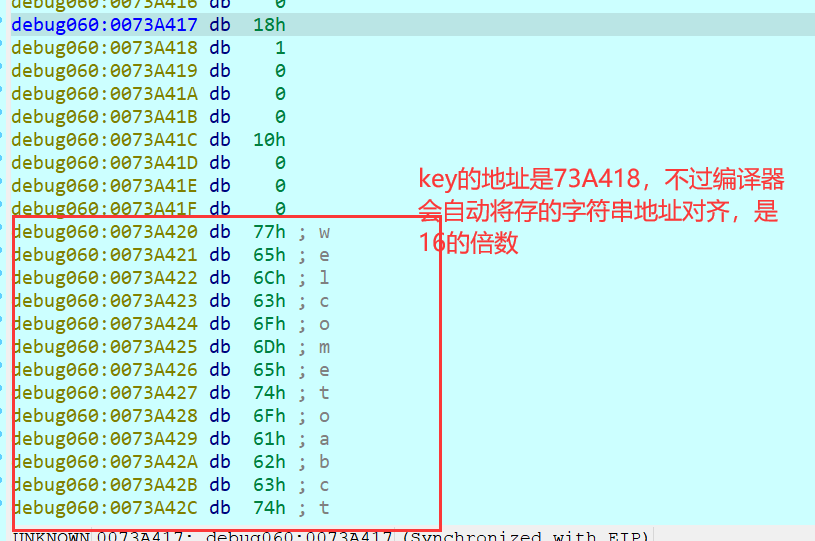
image-20240429183316170

62146

然而是个假flag

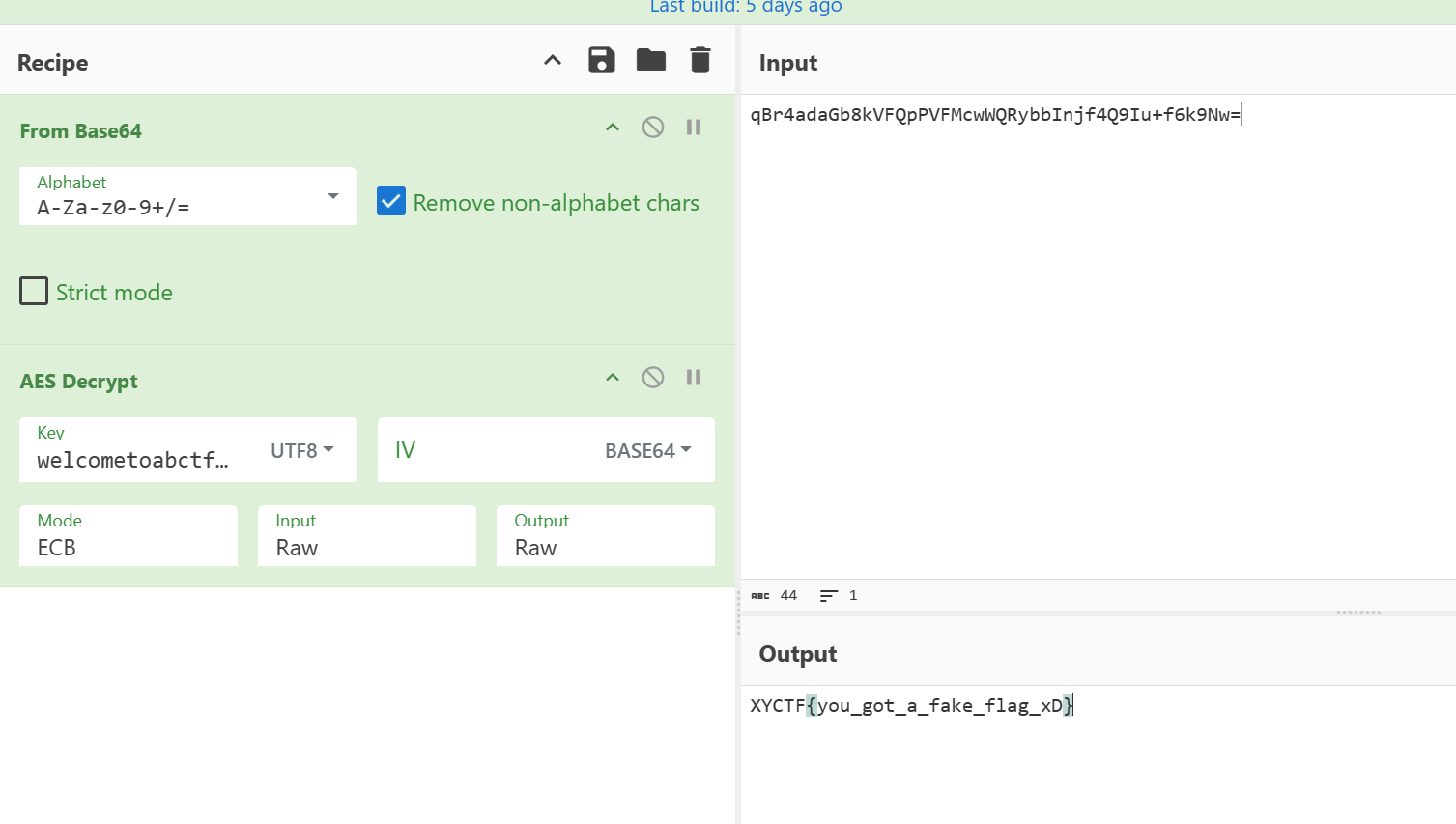
image-20240429183916672

综合多个wp，事实上这道题的情况是有一个反调试，如果检测到debugger的存在，就会给函数假数据和假key，其实这道题abctf已经给了提示了，我们就要想办法绕过这个反调

思路一是找到这个反调函数然后nop掉

思路二是用反反调试插件notify-bibi/ScyllaHide-IDA7.5: ScyllaHide for IDA7.5; ScyllaHide IDA7.5; It is a really niccccccce anti-anti-debug tool (github.com)

这道题的反调试比较简单，直接附加就可以绕过

然后重复以上的过程获得

key:welcometoxyctf!!

enc:RZy/zVEWMFxaCbzChAg8x26XZYr51rNVnM+zBoBp3gya93L9QQXpFRin1JE33vyx

from Crypto.Cipher import AES
import base64
enc=b'RZy/zVEWMFxaCbzChAg8x26XZYr51rNVnM+zBoBp3gya93L9QQXpFRin1JE33vyx'
enc_b64decode=base64.b64decode(enc.decode('utf-8'))
print(enc_b64decode)
key=b'welcometoxyctf!!'
cipher=AES.new(key,AES.MODE_ECB)
print(cipher.decrypt(enc_b64decode))
#b'XYCTF{y0u_@r3_v3ry_g00d_a7_E_l@ngu@ge}\n\n\n\n\n\n\n\n\n\n'

ezmath

py程序直接解包反编译一条龙

需要注意的是：用的python版本最好跟需要反编译的pyc版本一致，否则可能导致少部分信息缺失

# uncompyle6 version 3.9.1
# Python bytecode version base 3.8.0 (3413)
# Decompiled from: Python 3.11.5 | packaged by Anaconda, Inc. | (main, Sep 11 2023, 13:26:23) [MSC v.1916 64 bit (AMD64)]
# Embedded file name: ezmath.py
flag = [ord(i) for i in input("flag:")]
if len(flag) == 32:
    if (
        sum([flag[23] for _ in range(flag[23])])
        + sum([flag[12] for _ in range(flag[12])])
        + sum([flag[1] for _ in range(flag[1])])
        - sum([flag[24] for _ in range(222)])
        + sum([flag[22] for _ in range(flag[22])])
        + sum([flag[31] for _ in range(flag[31])])
        + sum([flag[26] for _ in range(flag[26])])
        - sum([flag[9] for _ in range(178)])
        - sum([flag[29] for _ in range(232)])
        + sum([flag[17] for _ in range(flag[17])])
        - sum([flag[23] for _ in range(150)])
        - sum([flag[6] for _ in range(226)])
        - sum([flag[7] for _ in range(110)])
        + sum([flag[19] for _ in range(flag[19])])
        + sum([flag[2] for _ in range(flag[2])])
        - sum([flag[0] for _ in range(176)])
        + sum([flag[10] for _ in range(flag[10])])
        - sum([flag[12] for _ in range(198)])
        + sum([flag[24] for _ in range(flag[24])])
        + sum([flag[9] for _ in range(flag[9])])
        - sum([flag[3] for _ in range(168)])
        + sum([flag[8] for _ in range(flag[8])])
        - sum([flag[2] for _ in range(134)])
        + sum([flag[14] for _ in range(flag[14])])
        - sum([flag[13] for _ in range(170)])
        + sum([flag[4] for _ in range(flag[4])])
        - sum([flag[10] for _ in range(142)])
        + sum([flag[27] for _ in range(flag[27])])
        + sum([flag[15] for _ in range(flag[15])])
        - sum([flag[15] for _ in range(224)])
        + sum([flag[16] for _ in range(flag[16])])
        - sum([flag[11] for _ in range(230)])
        - sum([flag[1] for _ in range(178)])
        + sum([flag[28] for _ in range(flag[28])])
        - sum([flag[5] for _ in range(246)])
        - sum([flag[17] for _ in range(168)])
        + sum([flag[30] for _ in range(flag[30])])
        - sum([flag[21] for _ in range(220)])
        - sum([flag[22] for _ in range(212)])
        - sum([flag[16] for _ in range(232)])
        + sum([flag[25] for _ in range(flag[25])])
        - sum([flag[4] for _ in range(140)])
        - sum([flag[31] for _ in range(250)])
        - sum([flag[28] for _ in range(150)])
        + sum([flag[11] for _ in range(flag[11])])
        + sum([flag[13] for _ in range(flag[13])])
        - sum([flag[14] for _ in range(234)])
        + sum([flag[7] for _ in range(flag[7])])
        - sum([flag[8] for _ in range(174)])
        + sum([flag[3] for _ in range(flag[3])])
        - sum([flag[25] for _ in range(242)])
        + sum([flag[29] for _ in range(flag[29])])
        + sum([flag[5] for _ in range(flag[5])])
        - sum([flag[30] for _ in range(142)])
        - sum([flag[26] for _ in range(170)])
        - sum([flag[19] for _ in range(176)])
        + sum([flag[0] for _ in range(flag[0])])
        - sum([flag[27] for _ in range(168)])
        + sum([flag[20] for _ in range(flag[20])])
        - sum([flag[20] for _ in range(212)])
        + sum([flag[21] for _ in range(flag[21])])
        + sum([flag[6] for _ in range(flag[6])])
        + sum([flag[18] for _ in range(flag[18])])
        - sum([flag[18] for _ in range(178)])
        + 297412
        == 0
    ):
        print("yes")

有佬用z3解

from z3 import *

# 创建⼀个Z3求解器
solver = Solver()
# 定义32个32位的变量
flag0 = Real('flag0')
flag1 = Real('flag1')
flag2 = Real('flag2')
flag3 = Real('flag3')
flag4 = Real('flag4')
flag5 = Real('flag5')
flag6 = Real('flag6')
flag7 = Real('flag7')
flag8 = Real('flag8')
flag9 = Real('flag9')
flag10 = Real('flag10')
flag11 = Real('flag11')
flag12 = Real('flag12')
flag13 = Real('flag13')
flag14 = Real('flag14')
flag15 = Real('flag15')
flag16 = Real('flag16')
flag17 = Real('flag17')
flag18 = Real('flag18')
flag19 = Real('flag19')
flag20 = Real('flag20')
flag21 = Real('flag21')
flag22 = Real('flag22')
flag23 = Real('flag23')
flag24 = Real('flag24')
flag25 = Real('flag25')
flag26 = Real('flag26')
flag27 = Real('flag27')
flag28 = Real('flag28')
flag29 = Real('flag29')
flag30 = Real('flag30')
flag31 = Real('flag31')
solver.add((flag23 * flag23) + (flag12 * flag12) + (flag1 * flag1) -
           (222 * flag24) + (flag22 * flag22) + (flag31 * flag31) + (flag26 *
                                                                     flag26) - (178 * flag9) - (232 * flag29) + (
                   flag17 * flag17) - (150 *
                                       flag23) - (226 * flag6) - (110 * flag7) + (flag19 * flag19) + (flag2 *
                                                                                                      flag2) - (
                   176 * flag0) + (flag10 * flag10) - (198 * flag12) + (flag24 *
                                                                        flag24) + (flag9 * flag9) - (
                   168 * flag3) + (flag8 * flag8) - (134 *
                                                     flag2) + (flag14 * flag14) - (170 * flag13) + (
                   flag4 * flag4) - (142 *
                                     flag10) + (flag27 * flag27) + (flag15 * flag15) - (224 * flag15) +
           (flag16 * flag16) - (230 * flag11) - (178 * flag1) + (flag28 * flag28) -
           (246 * flag5) - (168 * flag17) + (flag30 * flag30) - (220 * flag21) -
           (212 * flag22) - (232 * flag16) + (flag25 * flag25) - (140 * flag4) -
           (250 * flag31) - (150 * flag28) + (flag11 * flag11) + (flag13 * flag13) - (234 * flag14) + (
                   flag7 * flag7) - (174 * flag8) + (flag3 * flag3) -
           (242 * flag25) + (flag29 * flag29) + (flag5 * flag5) - (142 * flag30) -
           (170 * flag26) - (176 * flag19) + (flag0 * flag0) - (168 * flag27) +
           (flag20 * flag20) - (212 * flag20) + (flag21 * flag21) + (flag6 * flag6)
           + (flag18 * flag18) - (178 * flag18) + 297412 == 0)
# 检查是否存在解
# if solver.check() == sat:

# # 获取解
#     model = solver.model()
if solver.check()==sat:
    model=solver.model()
    print(model)
    list=[88, 89, 67, 84, 70, 123, 113, 55, 87, 89, 71, 115, 99, 85, 117, 112, 116, 84, 89, 88, 106, 110, 106, 75, 111, 121, 85, 84, 75, 116, 71, 125]
    for i in list:
        print(chr(i),end='')
        #XYCTF{q7WYGscUuptTYXjnjKoyUTKtG}
else:
    print("No solution")

有点迷惑z3的变量设置了，因为用Int会跑很久，Real几秒出

所以该如何声明什么类型的变量，如何判断？

思路二是观察然后化简

if len(flag) == 32 and (
 (flag[0] * (flag[0] - 176)) +
 (flag[1] * (flag[1] - 178)) +
 (flag[2] * (flag[2] - 134)) +
 (flag[3] * (flag[3] - 168)) +
 (flag[4] * (flag[4] - 140)) +
 (flag[5] * (flag[5] - 246)) +
 (flag[6] * (flag[6] - 226)) +
 (flag[7] * (flag[7] - 110)) +
 (flag[8] * (flag[8] - 174)) +
 (flag[9] * (flag[9] - 178)) +
 (flag[10] * (flag[10] - 142)) +
 (flag[11] * (flag[11] - 230)) +
 (flag[12] * (flag[12] - 198)) +
 (flag[13] * (flag[13] - 170)) +
 (flag[14] * (flag[14] - 234)) +
 (flag[15] * (flag[15] - 224)) +
 (flag[16] * (flag[16] - 232)) +
 (flag[17] * (flag[17] - 168)) +
 (flag[18] * (flag[18] - 178)) +
 (flag[19] * (flag[19] - 176)) +
 (flag[20] * (flag[20] - 212)) +
 (flag[21] * (flag[21] - 220)) +
 (flag[22] * (flag[22] - 212)) +
 (flag[23] * (flag[23] - 150)) +
 (flag[24] * (flag[24] - 222)) +
 (flag[25] * (flag[25] - 242)) +
 (flag[26] * (flag[26] - 170)) +
 (flag[27] * (flag[27] - 168)) +
 (flag[28] * (flag[28] - 150)) +
 (flag[29] * (flag[29] - 232)) +
 (flag[30] * (flag[30] - 142)) +
 (flag[31] * (flag[31] - 250)) + 297412 == 0

通过观察可以发现，每一行后面减的数除以二就是flag

ez_cube

是一个魔方程序，先阅读一个类似的程序获得灵感

用C语言写一个数字版的3阶魔方_简单c语言程序判断3*3洛术魔方-CSDN博客

image-20240429200310554

所以只能逆如何把cube还原，是利用CFOP公式

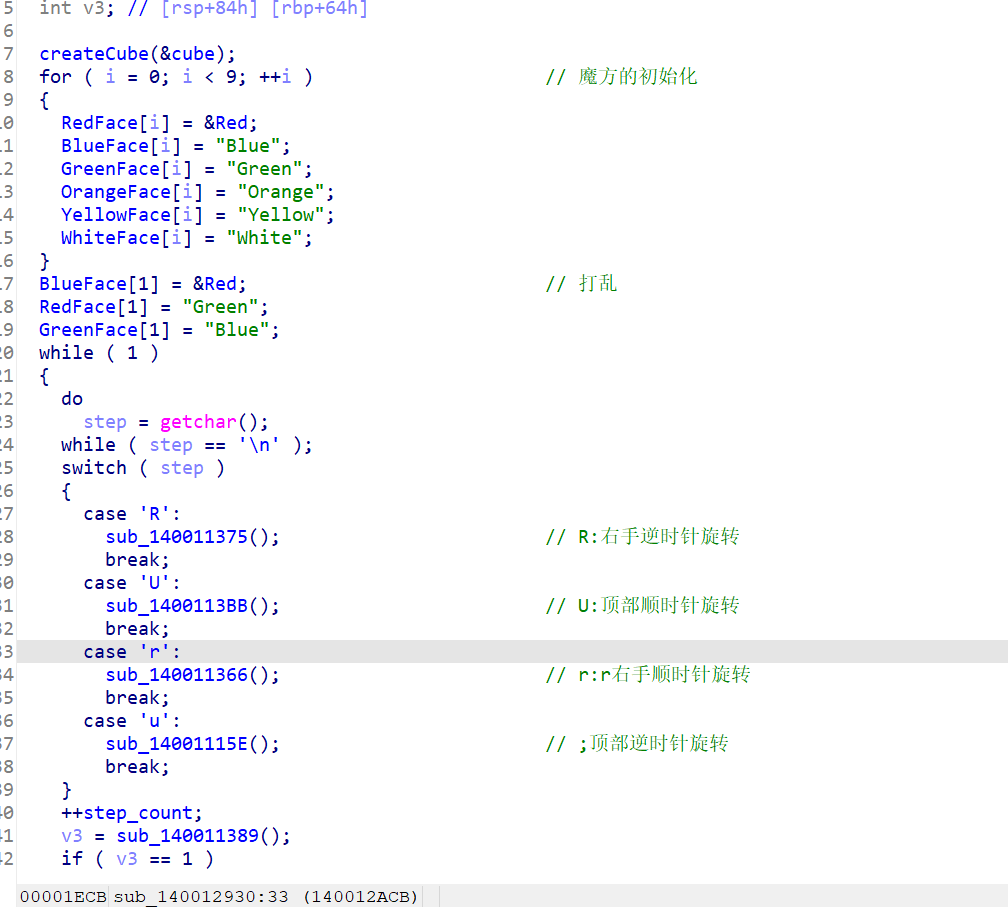
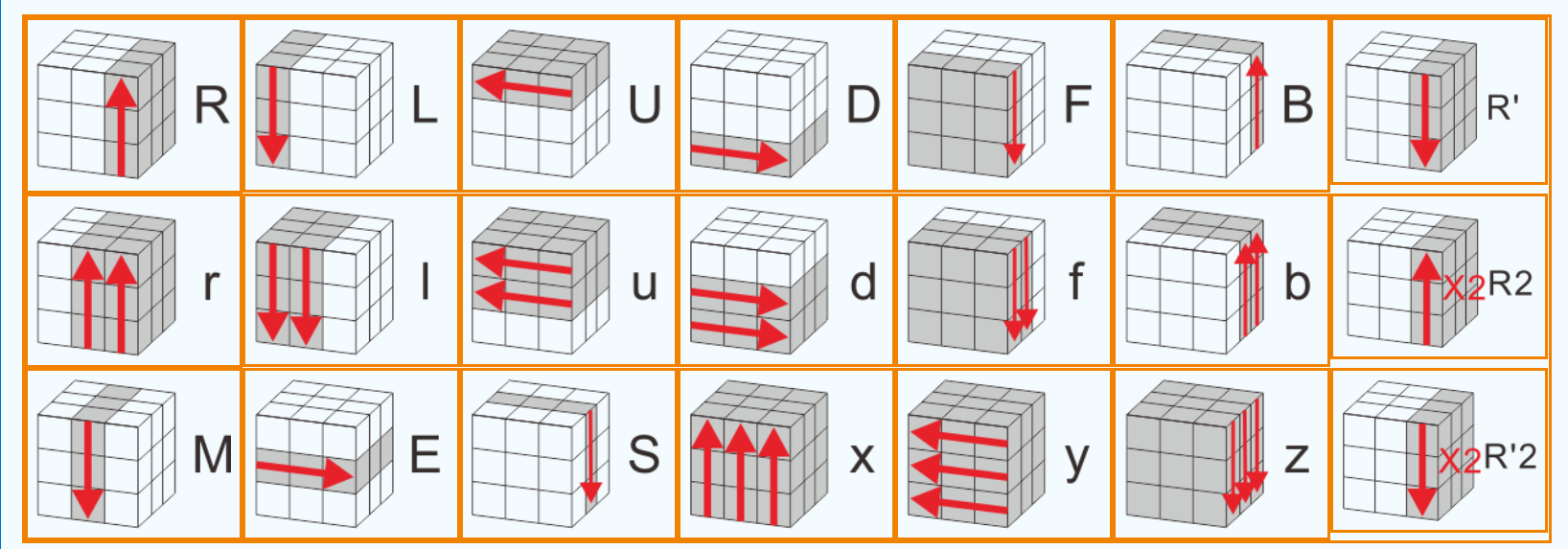
image-20240429205604162 image-20240429202333254

魔方求解器 (rubiks-cube-solver.com)

也可以用angr一把嗦,或者自己写脚本爆破

借鉴了一下dl的脚本

from itertools import *

red = [''] * 9
blue = [''] * 9
green = [''] * 9
orange = [''] * 9
yellow = [''] * 9
white = [''] * 9


def init_cube():
    for i in range(9):
        red[i] = "red"
        blue[i] = "blue"
        green[i] = "green"
        orange[i] = "orange"
        yellow[i] = "yellow"
        white[i] = "white"
    blue[1] = "red"
    red[1] = "green"
    green[1] = ("blue")


def MOVE_R():
    v1 = red[2]
    v2 = red[5]
    v3 = red[8]
    red[2] = white[2]
    red[5] = white[5]
    red[8] = white[8]
    white[2] = orange[6]
    white[5] = orange[3]
    white[8] = orange[0]
    orange[0] = yellow[8]
    orange[3] = yellow[5]
    orange[6] = yellow[2]
    yellow[2] = v1
    yellow[5] = v2
    yellow[8] = v3
    v4 = green[1]
    green[1] = green[3]
    green[3] = green[7]
    green[7] = green[5]
    green[5] = v4
    v5 = green[0]
    green[0] = green[6]
    green[6] = green[8]
    green[8] = green[2]
    green[2] = v5


def MOVE_U():
    v1 = red[0]
    v2 = red[1]
    v3 = red[2]
    red[0] = green[0]
    red[1] = green[1]
    red[2] = green[2]
    green[0] = orange[0]
    green[1] = orange[1]
    green[2] = orange[2]
    orange[0] = blue[0]
    orange[1] = blue[1]
    orange[2] = blue[2]
    blue[0] = v1
    blue[1] = v2
    blue[2] = v3
    v4 = yellow[1]
    yellow[1] = yellow[3]
    yellow[3] = yellow[7]
    yellow[7] = yellow[5]
    yellow[5] = v4
    v5 = yellow[0]
    yellow[0] = yellow[6]
    yellow[6] = yellow[8]
    yellow[8] = yellow[2]
    yellow[2] = v5


def MOVE_r():
    v1 = red[2]
    v2 = red[5]
    v3 = red[8]
    red[2] = yellow[2]
    red[5] = yellow[5]
    red[8] = yellow[8]
    yellow[2] = orange[6]
    yellow[5] = orange[3]
    yellow[8] = orange[0]
    orange[0] = white[8]
    orange[3] = white[5]
    orange[6] = white[2]
    white[2] = v1
    white[5] = v2
    white[8] = v3
    v4 = green[1]
    green[1] = green[5]
    green[5] = green[7]
    green[7] = green[3]
    green[3] = v4
    v5 = green[0]
    green[0] = green[2]
    green[2] = green[8]
    green[8] = green[6]
    green[6] = v5


def MOVE_u():
    v1 = red[0]
    v2 = red[1]
    v3 = red[2]
    red[0] = blue[0]
    red[1] = blue[1]
    red[2] = blue[2]
    blue[0] = orange[0]
    blue[1] = orange[1]
    blue[2] = orange[2]
    orange[0] = green[0]
    orange[1] = green[1]
    orange[2] = green[2]
    green[0] = v1
    green[1] = v2
    green[2] = v3
    v4 = yellow[1]
    yellow[1] = yellow[5]
    yellow[5] = yellow[7]
    yellow[7] = yellow[3]
    yellow[3] = v4
    v5 = yellow[0]
    yellow[0] = yellow[2]
    yellow[2] = yellow[8]
    yellow[8] = yellow[6]
    yellow[6] = v5


def is_right():
    flag=1
    for i in range(9):
        if red[i]!="red":
            flag=0
        if blue[i]!="blue":
            flag=0
        if green[i]!="green":
            flag=0
        if orange[i]!="orange":
            flag=0
        if yellow[i]!="yellow":
            flag=0
        if white[i]!="white":
            flag=0
    return flag

def main(flag):
    print(flag)
    init_cube()
    for i in flag:
        if i=="R":
            MOVE_R()
        if i=="U":
            MOVE_U()
        if i=="r":
            MOVE_r()
        if i=="u":
            MOVE_u()
    if is_right():
        return flag

def get_flag():
    table="RrUu"
    for string in product(table,repeat=12):
        flag="".join(string)
        ret=main(flag)
        if ret !=None:
            print(ret)
            return
get_flag()
#RuRURURuruRR

砸核桃

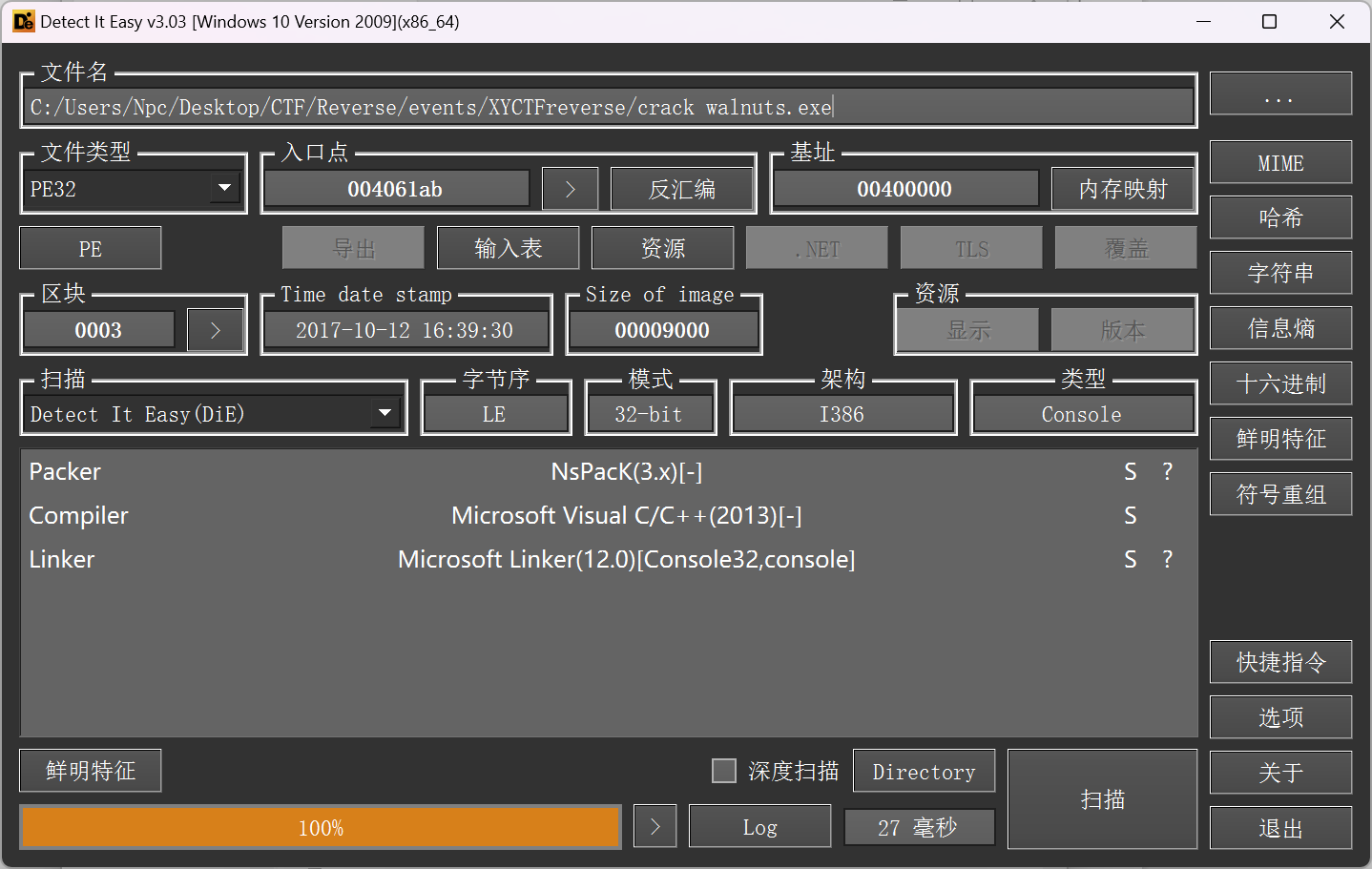
image-20240429205814345

ASP壳，用od脱一下壳

[原创]新手 NsPacK3.7 脱壳记录-加壳脱壳-看雪-安全社区|安全招聘|kanxue.com

4.2 寻找OEP
经过修改后的 PE 文件已经可以正常识别了，同样也显示出相应的编译信息与壳的信息，NsPacK V3.7 中文名称为北斗壳，是国内人编写的压缩壳。既然是手工对其脱壳，自然第一步就是寻找 OEP（原始入口点）。
ollydbg 载入后入口点处为：pushfd，pushad，call XXXX
OEP 的特征如下：popad，popfd，jmp OEP

我采用了搜索popfd打断点 不断F9到OEP的位置

然后按照教程fixdump得到主函数（现在对windowsPE结构不太懂，不了解为什么要按照这个步骤来，以后有时间进行学习

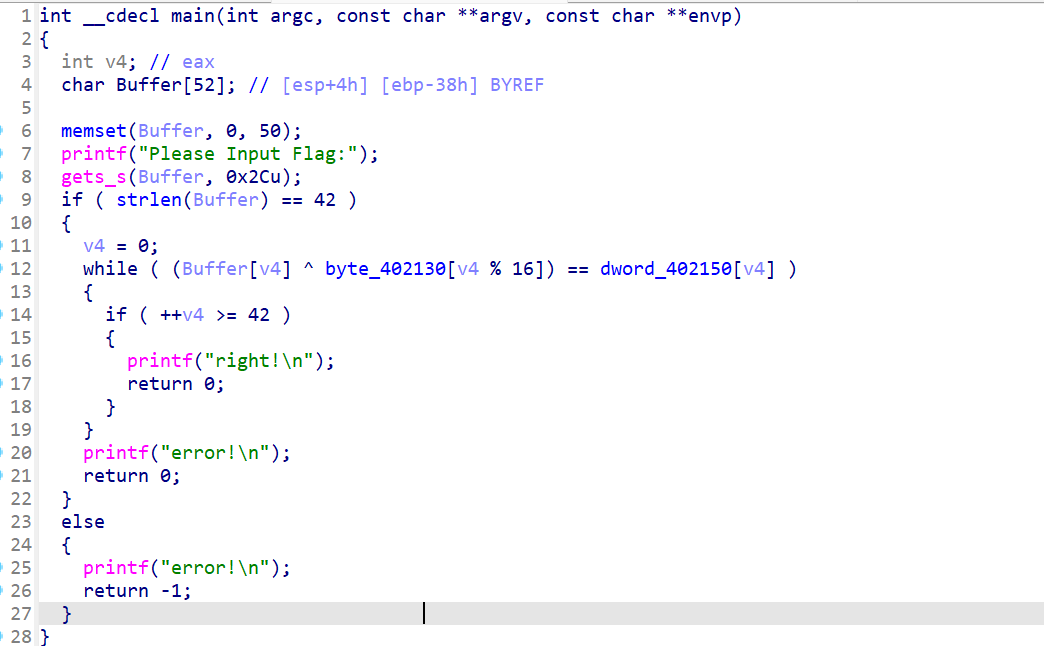
image-20240429212703953

发现是个简单的异或

flag=""
key=[0x74, 0x68, 0x69, 0x73, 0x5F, 0x69, 0x73, 0x5F, 0x6E, 0x6F, 0x74, 0x5F, 0x66, 0x6C, 0x61, 0x67]
enc=[0x00000012, 0x00000004, 0x00000008, 0x00000014, 0x00000024, 0x0000005C, 0x0000004A, 0x0000003D, 0x00000056, 0x0000000A, 0x00000010, 0x00000067, 0x00000000, 0x00000041, 0x00000000, 0x00000001, 0x00000046, 0x0000005A, 0x00000044, 0x00000042, 0x0000006E, 0x0000000C, 0x00000044, 0x00000072, 0x0000000C, 0x0000000D, 0x00000040, 0x0000003E, 0x0000004B, 0x0000005F, 0x00000002, 0x00000001, 0x0000004C, 0x0000005E, 0x0000005B, 0x00000017, 0x0000006E, 0x0000000C, 0x00000016, 0x00000068, 0x0000005B, 0x00000012, 0x00000000, 0x00000000, 0x00000048]
print(len(enc))
for i in range(42):
    flag+=chr(enc[i]^key[i%16])
print(flag)
# flag{59b8ed8f-af22-11e7-bb4a-3cf862d1ee75}

ez_enc

scanf(&input, input_);
for ( i = 0; i < (int)(j_strlen(input_) - 1); ++i )
  input_[i] = aImouto[i % 6] ^ (input_[i + 1] + (unsigned __int8)input_[i] % 20);
for ( j = 0; j < (int)j_strlen(input_); ++j )
{
  if ( input_[j] != byte_14001E008[j] )
  {
    printf("Wrong");
    return 0;
  }
}
printf("Right,but where is my Imouto?\n");

摘录关键逻辑

逆向解的话有两个思路，⼀是通过倒序解 Str[i] ，但 Str[i] 取了模存在信息丢失，很难解）需要爆破；⼆是通过正序解 Str[i+1] ，这个需要知道 Str[0] 就能递推。经过 ⼿动解前⼏个得出开头为 flag{ ，因此 Str[0] 就是 f

思路一的exp;

target = [0x27, 0x24, 0x17, 0x0B, 0x50, 0x03, 0xC8, 0x0C, 0x1F, 0x17, 0x36,
 0x55, 0xCB, 0x2D, 0xE9, 0x32, 0x0E, 0x11, 0x26, 0x02, 0x0C, 0x07, 0xFC,
 0x27, 0x3D, 0x2D, 0xED, 0x35, 0x59, 0xEB, 0x3C, 0x3E, 0xE4, 0x7D ]
aImouto =[0x49, 0x4D, 0x6F, 0x75, 0x74, 0x6F]
flag = [0]*len(target)
flag[len(target)-1] = target[len(target)-1]
print(flag)
def checkflag(idx,result):
    if(idx==-1):
        print("flag：爆破成功!")
        for i in range(len(result)):
            print(chr(result[i]),end="")
        print("")
        result
    for ch1 in range(128):
        if target[idx]==(aImouto[idx%6]^(result[idx+1]+ch1%20)):
            result[idx]=ch1
            checkflag(idx-1,result)
            checkflag(idx-1,result)
        if(ch1==128 and result[idx]==0):
            return
checkflag(32,flag)

思路二的exp

enc=[0x27, 0x24, 0x17, 0x0B, 0x50, 0x03, 0xC8, 0x0C, 0x1F, 0x17, 0x36, 0x55, 0xCB, 0x2D, 0xE9, 0x32, 0x0E, 0x11, 0x26, 0x02, 0x0C, 0x07, 0xFC, 0x27, 0x3D, 0x2D, 0xED, 0x35, 0x59, 0xEB, 0x3C, 0x3E, 0xE4, 0x7D]
flag=""
# """ 正向逻辑：
# for i in range(len(input)-1)
# enc[i]=Imouto[i%6]^(input[i+1]+input[i]%20)

# enc[len(input)-1]=input[len(input)-1]

# chr(0x7D)='}'

# 那么我们就可以逆向求解
# from string import printable
# input 都是可读字符
key='IMouto'
flag=[0]*len(enc)
flag[0]=ord('f')
for i in range(0,len(enc)-1):
    flag[i+1]=((enc[i] ^ ord(key[i % 6])) - flag[i] % 20) & 0xff
    # flag[i+1]=((enc[i]-flag[i]%20)^ord(key[i%6]))&0xff

for i in flag:
    print(chr(i),end="" )
#减法优先级高于异或

z3的解法

 from prism import *
 key = 'IMouto
 last = [0x27, 0x24, 0x17, 0x0B, 0x50, 0x03, 0xC8, 0x0C,
 0x1F, 0x17, 0x36, 0x55, 0xCB, 0x2D, 0xE9, 0x32,
 0x0E, 0x11, 0x26, 0x02, 0x0C, 0x07, 0xFC, 0x27,
 0x3D, 0x2D, 0xED, 0x35, 0x59, 0xEB, 0x3C, 0x3E,
 0xE4, 0x7D]
out,flag = zini(34)
f = Solver()
for i in range(33):
	f.add(last[i]==(ord(key[i%6])^out[i+1]+out[i] % 20))
isflag(f,flag)
zcheck(f,flag)
 # flag{!_r3ea11y_w4nt_@_cu7e_s1$ter}

findme

die查看一下三个文件的信息，发现文件4可以打开

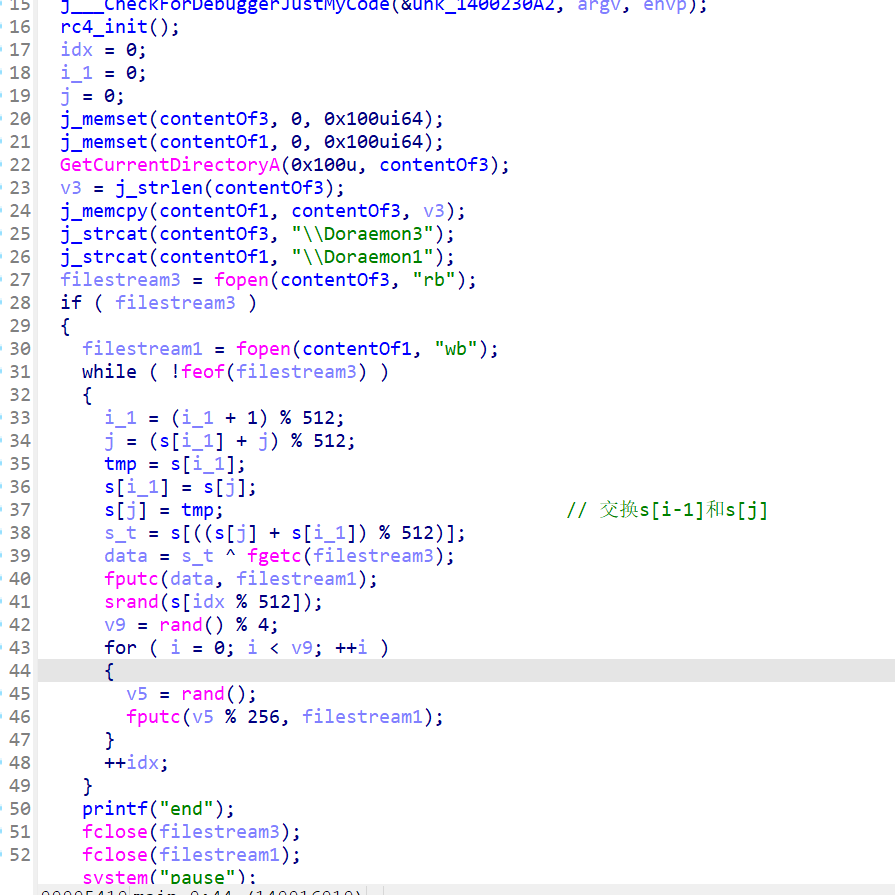
image-20240430230831871

可以分析出:首先进行rc4_init初始化一个512数组

然后打开Doraemon3文件读取文件流，然后逐字符进行rc4加密，并且以sbox[idx%512]作为伪随机数种子获得随机数，写入随机大小的垃圾数组得到filestream1。而题目只给了我们1,2没有给3，我们要先由文件1逆推得到3

  • 思路1:看了师傅们的wp，由于rc4是流加密，s[box]加密解密不变，因此加密和解密的伪随机数生成的也是一一样的，rc4解密好处理，关键是垃圾数据的去除。事实上只要把fputc给hook成fgetc就完美还原了文件解密的过程

​ 如何patch?

​ image-20240430232435453

image-20240430232454749

patch fputc的字节码为：FF 15 0B B0 00 00，

由于fgetc只需要1个参数且第一个参数存入rcx

fputc函数的调用第一个参数存入rcx，第二个参数存入的是rdx

patch后需要把rdx改为rcx然后nop掉中间将第一个参数传入rcx的指令就可以把第二个参数传入rcx当中并且正常运行了

因此要修改这四处地方，更换输入输出

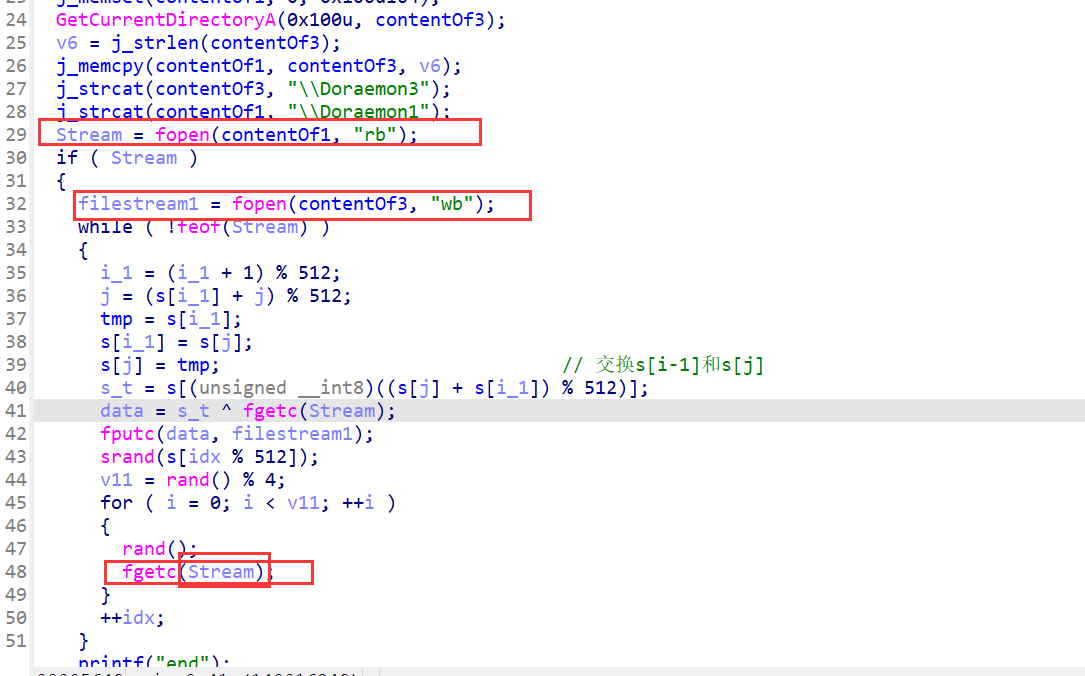
image-20240501010408892

  • 思路2：照着加密逻辑，写正向脚本，按照第一种思路把输入输出流给颠倒一下获得解密脚本,函数主体直接copy反编译的源码，然后稍微修改一下

    #include <stdio.h>
#include <string.h>

const char *Str = "Find_Doraemon";

unsigned char BOX[512];

void init_box()
{
    char *v0;        // rdi
    __int64 i;       // rcx
    char v3[32];     // [rsp+0h] [rbp-20h] BYREF
    char v4;         // [rsp+20h] [rbp+0h] BYREF
    unsigned int v5; // [rsp+24h] [rbp+4h]
    char v6;         // [rsp+44h] [rbp+24h]
    char v7[532];    // [rsp+70h] [rbp+50h] BYREF
    unsigned int j;  // [rsp+284h] [rbp+264h]
    int v9;          // [rsp+2A4h] [rbp+284h]
    int v10;         // [rsp+2C4h] [rbp+2A4h]

    v5 = strlen(Str);
    memset(v7, 0, 0x200);
    for (j = 0; j < 0x200; ++j)
    {
        v6 = j;
        BOX[j] = -(char)j;
        v7[j] = Str[j % v5];
    }
    v9 = 0;
    v10 = 0;
    while (v9 < 512)
    {
        v10 = ((unsigned __int8)v7[v9] + BOX[v9] + v10) % 512;
        unsigned char tmp = BOX[v9];
        BOX[v9] = BOX[v10];
        BOX[v10] = tmp;
        ++v9;
    }
}

int main()
{
    size_t v3;           // rax
    int v5;              // eax
    FILE *fout;        // [rsp+28h] [rbp+8h]
    FILE *fin;            // [rsp+48h] [rbp+28h]
    int v8;              // [rsp+64h] [rbp+44h]
    int v9;              // [rsp+84h] [rbp+64h]
    int v10;             // [rsp+A4h] [rbp+84h]
    int v11;             // [rsp+C4h] [rbp+A4h]
    unsigned __int8 v12; // [rsp+104h] [rbp+E4h]
    unsigned __int8 v13; // [rsp+144h] [rbp+124h]
    int i;               // [rsp+164h] [rbp+144h]

    init_box();
    v8 = 0;
    v10 = 0;
    v11 = 0;
    fout = fopen("Doraemon3", "wb");
    fin = fopen("Doraemon1", "rb");
    while (!feof(fin))
    {
        v10 = (v10 + 1) % 512;
        v11 = (BOX[v10] + v11) % 512;
        unsigned char tmp = BOX[v10];
        BOX[v10] = BOX[v11];
        BOX[v11] = tmp;
        v13 = BOX[(unsigned __int8)((BOX[v11] + BOX[v10]) % 512)];
        v12 = v13 ^ fgetc(fin);
        fputc(v12, fout);
        srand(BOX[v8 % 512]);
        v9 = rand() % 4;
        for (i = 0; i < v9; ++i)
        {
            v5 = rand();
            fgetc(fin);
        }
        ++v8;
    }
    fclose(fout);
    fclose(fin);

    return 0;
}

最后获得3是个解密程序，用于解密2直接执行即可

image-20240501011131014

用010editor打开发现GIF89a是gif头,修改拓展名然后打开即可

image-20240501011335998

今夕是何年

与TCPL类似，用qemu搭建龙芯环境即可

win11 使用 QEMU 配置龙芯 3A5000 虚拟环境_qemu 龙芯-CSDN博客

熟悉qemu的用法吧

What’s this

拖进die，发现是lua编译

Lua Decompiler (metaworm.site)

Lua 工具箱 (luatool.cn)

找个在线网站反编译一下

或者找在线工具

viruscamp/luadec: Lua Decompiler for lua 5.1 , 5.2 and 5.3 (github.com)

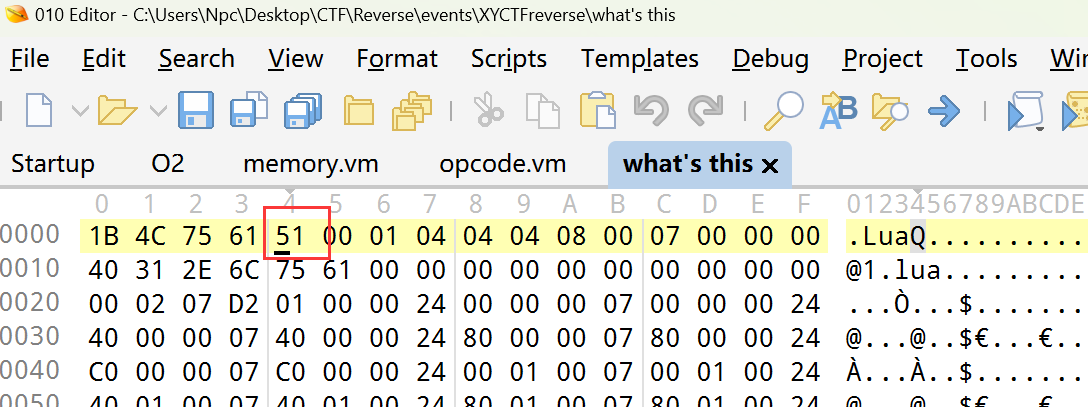
image-20240501013114589

魔术数字51可判断版本为lua5.1

反编译的lua脚本经过混淆了，

抓取关键逻辑

Xor = function(num1, num2)
  -- function num : 0_109
  local tmp1 = num1
  local tmp2 = num2
  local str = ""
  repeat
    repeat
      local s1 = tmp1 % 2
      local s2 = tmp2 % 2
      if s1 == s2 then
        str = "0" .. str
      else
        str = "1" .. str
      end
      tmp1 = (math.modf)(tmp1 / 2)
      tmp2 = (math.modf)(tmp2 / 2)
    until tmp1 == 0
  until tmp2 == 0
  return tonumber(str, 2)
end

value = ""
output = ""
i = 1
while 1 do
  local temp = (string.byte)(flag, i)
  temp = (string.char)(Xor(temp, 8) % 256)
  value = value .. temp
  i = i + 1
  if (string.len)(flag) < i then
    break
  end
end
do
  for _ = 1, 1000 do
    x = 3
    y = x * 3
    z = y / 4
    w = z - 5
    if w == 0 then
      print("This line will never be executed")
    end
  end
  for i = 1, (string.len)(flag) do
    temp = (string.byte)(value, i)
    temp = (string.char)(temp + 3)
    output = output .. temp
  end
  result = output:rep(10)
  invalid_list = {1, 2, 3}
  for _ = 1, 20 do
    (table.insert)(invalid_list, 4)
  end
  for _ = 1, 50 do
    result = result .. "A"
    ;
    (table.insert)(invalid_list, 4)
  end
  for i = 1, (string.len)(output) do
    temp = (string.byte)(output, i)
    temp = (string.char)(temp - 1)
  end
  for _ = 1, 30 do
    result = result .. (string.lower)(output)
  end
  for _ = 1, 950 do
    x = 3
    y = x * 3
    z = y / 4
    w = z - 5
    if w == 0 then
      print("This line will never be executed")
    end
  end
  for _ = 1, 50 do
    x = -1
    y = x * 4
    z = y / 2
    w = z - 3
    if w == 0 then
      print("This line will also never be executed")
    end
  end
  require("base64")
  obfuscated_output = to_base64(output)
  obfuscated_output = (string.reverse)(obfuscated_output)
  obfuscated_output = (string.gsub)(obfuscated_output, "g", "3")
  obfuscated_output = (string.gsub)(obfuscated_output, "H", "4")
  obfuscated_output = (string.gsub)(obfuscated_output, "W", "6")
  invalid_variable = obfuscated_output:rep(5)
  if obfuscated_output == "==AeuFEcwxGPuJ0PBNzbC16ctFnPB5DPzI0bwx6bu9GQ2F1XOR1U" then
    print("You get the flag.")
  else
    print("F**k!")
  end
end

flag 每字节与8异或，然后加3,转为base64，逆置，然后进行字符替换写一个脚本逆过来即可

import base64

enc="==AeuFEcwxGPuJ0PBNzbC16ctFnPB5DPzI0bwx6bu9GQ2F1XOR1U"
newenc=enc.replace("3","g").replace("4","H").replace("6","W")
newenc=newenc[::-1]
print(newenc)
newenc2=base64.b64decode(newenc)
print(newenc2)
for i in newenc2:
    print(chr(((i-3)^0x8)&0xff),end="")
# U1ROX1F2QG9ubWxwb0IzPD5BPnFtcW1CbzNBP0JuPGxwcEFueA==
# b'STN_Qv@onmlpoB3<>A>qmqmBo3A?Bn<lppAnx'
# XYCTF{5dcbaed781363fbfb7d8647c1aee6c}

ezrand

image-20240501105646687

可以看出随机数的seed与时间有关，获得的随机数再与输入的flag进行一些列操作获得密文，但是rand_number是unsigned int8类型，我们可以对seed进行爆破

rand 函数在api-ms-win-crt-utility-l1-1-0 ）总是返回一个范围是 16 位的整数。 为确保爆破用的 rand 同样是来自 api-ms-win-crt-utility-l1-1-0 的

坑：这里的伪代码是有问题的，这⾥并⾮直接调⽤srand(time64(0)) ⽽是中间⽤了个 movzx ecx,ax; 实际上就是保留了低16位 即真正的随机数种⼦是time64(0)&0xf

#include <stdio.h>
#include <stdlib.h>
#define u8 unsigned char
#define u16 unsigned short
#define u32 unsigned int
#define u64 unsigned long long
u8 ida_chars[] =
{
    0x5D, 0x0C, 0x6C, 0xEA, 0x46, 0x19, 0xFC, 0x34, 0xB2, 0x62,
    0x23, 0x07, 0x62, 0x22, 0x6E, 0xFB, 0xB4, 0xE8, 0xF2, 0xA9,
    0x91, 0x12, 0x21, 0x86, 0xDB, 0x8E, 0xE9, 0x43, 0x4D };

const char* tmpl = "XYCTF{XXXXXXXXXXXXXXXXXXXXXX}";

int main() {
    for (u32 i = 0; i <= 0xFFFF; i++) {
        u32 flag = 1;
        srand(i);
        for (int j = 0; j < 29; j++) {
            u32 eax = rand(); // 16 bits
            u32 r8d = eax;
            u64 mul = (u64)eax * (u64)0x80808081;
            u32 edx = (mul >> 32) >> 7;
            u32 ecx;
            // always 0:
            // ecx = edx >> 31;
            // edx += ecx;
            ecx = edx * 0xFF;
            r8d -= ecx;
            r8d ^= ida_chars[j];
            if (j < 6 || j == 28) {
                if (r8d != tmpl[j]) {
                    flag = 0;
                    break;
                }
            }
            // or:
            // if (r8d < 32 || r8d >= 127) {
            //     flag = 0;
            //     break;
            // }
        }
        if (flag) {
            printf("Seed: %u\t", i);
            srand(i);
            for (int j = 0; j < 29; j++) {
                u32 eax = rand();
                u32 r8d = eax;
                u64 mul = (u64)eax * (u64)0x80808081;
                u32 edx = (mul >> 32) >> 7;
                u32 ecx;
                ecx = edx * 0xFF;
                r8d -= ecx;
                r8d ^= ida_chars[j];
                printf("%c", r8d);
            }
            printf("\n");
            
        }
    }
}

给阿姨倒一杯卡布奇诺

魔改tea加密，稍微修改一下tea的模版即可

#include <stdio.h>
#define uint32_t unsigned int

void decrypt(uint32_t* v, uint32_t* key)
{
    static uint32_t data1 = 0x5F797274;
    static uint32_t data2 = 0x64726168;
    int i;   // [rsp+20h] [rbp-10h]
    uint32_t sum; // [rsp+24h] [rbp-Ch]
    uint32_t v1;  // [rsp+28h] [rbp-8h]
    uint32_t v0;  // [rsp+2Ch] [rbp-4h]

    sum = 0x6E75316C * 32;
    uint32_t data1_tmp = v[0];
    uint32_t data2_tmp = v[1];
    v0 = v[0];
    v1 = v[1];
    for (i = 31; i >= 0; i--)
    {
        v1 -= ((v0 >> 5) + key[3]) ^ (v0 + sum) ^ (key[2] + 16 * v0) ^ (sum + i);
        v0 -= ((v1 >> 5) + key[1]) ^ (v1 + sum) ^ (key[0] + 16 * v1) ^ (sum + i);
        sum -= 0x6E75316C;
    }
    v[0] = v0 ^ data1;
    v[1] = v1 ^ data2;
    data1 = data1_tmp;
    data2 = data2_tmp;
}

int main()
{
    uint32_t key[4];   // [rsp+60h] [rbp-40h] BYREF
    uint32_t array[8]; // [rsp+70h] [rbp-30h]
    array[0] = 0x9B28ED45;
    array[1] = 0x145EC6E9;
    array[2] = 0x5B27A6C3;
    array[3] = 0xE59E75D5;
    array[4] = 0xE82C2500;
    array[5] = 0xA4211D92;
    array[6] = 0xCD8A4B62;
    array[7] = 0xA668F440;
    key[0] = 0x65766967;
    key[1] = 0x756F795F;
    key[2] = 0x7075635F;
    key[3] = 0x6165745F;
    for (int i = 0; i <= 7; i += 2)
    {
        decrypt(array + i, key);
    }
    for (int i = 0; i < 32; i++)
    {
        printf("%c", ((char*)array)[i]);
    }
    return 0;
}

馒头

数据结构哈夫曼树的构建和解码

//大概的正向流程
typedef struct
{
    int data;
    int weight;
    int parent;
    int lch;
    int rch;
} htNode;

typedef htNode *huffmanTree;

int initHuffmanTree(huffmanTree *HT)
{
    *HT = (huffmanTree)malloc(960);
    for (int i = 1; i <= 47; ++i)  
    {
        (*HT)[i].parent = (*HT)[i].lch = (*HT)[i].rch = -1;
    }
    puts("please input flag:");
    for (int i_0 = 1; i_0 <= 24; ++i_0)  
    {
        (*HT)[i_0].data = i_0;
        (*HT)[i_0].weight = getchar();
    }
    return 1;
}

void creatHuffmanTree(huffmanTree *HT, int n)
{
    int j;      // [rsp+8h] [rbp-18h]
    int rnode;  // [rsp+Ch] [rbp-14h]
    int min2;   // [rsp+10h] [rbp-10h]
    int lnode;  // [rsp+14h] [rbp-Ch]
    int min1;   // [rsp+18h] [rbp-8h]
    int i;      // [rsp+1Ch] [rbp-4h]

    if (n > 1)
    {
        for (i = n + 1; i < 2 * n; ++i)  
        {
            min1 = 0x7FFF;
            lnode = -1;
            min2 = 0x7FFF;
            rnode = -1;
            for (j = 1; i > j; ++j)  // 找到两个最小的节点
            {
                if (min1 > (*HT)[j].weight && (*HT)[j].parent == -1)
                {
                    min2 = min1;
                    rnode = lnode;
                    min1 = (*HT)[j].weight;
                    lnode = j;
                }
                else if (min2 > (*HT)[j].weight && (*HT)[j].parent == -1)
                {
                    min2 = (*HT)[j].weight;
                    rnode = j;
                }
            }
            (*HT)[lnode].parent = (*HT)[rnode].parent = i;
            (*HT)[i].lch = lnode;
            (*HT)[i].rch = rnode;
            (*HT)[i].weight = (*HT)[lnode].weight + (*HT)[rnode].weight;
        }
    }
}

int ans1[58] = { 2270, 917, 446, 217, 106, 51, 20, 15, 17, 229, 114, 16, 11, 471, 233, 116, 14, 13, 238, 118, 12, 7, 1353, 557, 248, 123, 6, 24, 309, 137, 67, 3, 5, 172, 84, 4, 1, 796, 383, 186, 89, 2, 8, 197, 97, 48, 23, 10, 21, 413, 203, 101, 22, 9, 210, 104, 19, 18 };

int check_flag(huffmanTree HT, int i)
{
    static int index = 0;
    if (i <= 24)  // 对于叶子，只比对下标
    {
        if (HT[i].data != ans1[index++])
            return 0;
    }
    else 
    {
        if (HT[i].weight != ans1[index++])
            return 0;
        if (HT[HT[i].lch].data <= 24 && HT[HT[i].lch].data > 0)
        {
            if (HT[HT[i].lch].weight != ans1[index++])
                return 0;
        }
    }
    if (HT[i].lch <= 0)  
        return 1;
    return check_flag(HT, HT[i].lch) && check_flag(HT, HT[i].rch);  
}

由于每个叶子节点权值不会小于32，手画一下huffmantree就可以了

舔狗四部曲 – 我的白月光