Reference

AES - CTF Wiki (ctf-wiki.org)

https://en.wikipedia.org/wiki/Advanced_Encryption_Standard

Rijndael S-box - Wikipedia

仅用作学习记录，归纳总结

块加密

块密码/分组密码

常见的块加密算法有

  • IDEA加密
  • DES加密
  • AES加密

块加密是对称密钥算法，将明文分为多个等长的模块（block）

然后使用确定的算法和对称密钥对每组分别加密解密

分组加密包含两个成对的算法：加密算法EE和解密算法DD,两者互为反函数。每个算法有两个输入：长度为n位的组，和长度为k位的密钥；两组输入均生成n位输出。将两个算法看做函数，KK表示长度为kk的密钥（密钥长度），PP表示长度为nn的分组,PP也被飘逝为明文，CC表示密文，

则满足：

EK(P)=C  ;EK−1(C)=PE_K(P) = C \; ; \quad E_K^{-1}(C)=P

EK(P):=E(K,P):{0,1}k×{0,1}n→{0,1}n,E_K(P) := E(K,P): \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n,

对于任意密钥 KK,EK(P)E_K(P)是输入的组的一个置换函数，且可逆地落在0,1n{0,1}^n区间。E的反函数（解密算法）定义为：

EK−1(C):=DK(C)=D(K,C):{0,1}k×{0,1}n→{0,1}n,E_K^{-1}(C) := D_K(C) = D(K,C): \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n,

所谓加密解密，就是由密钥生成的box进行替换，每次替换就是替换的一个block，比如一个分组加密算法使用一段 128 位的分组作为明文，相应输出 128 位的密文；而其转换则受加密算法中第二个输入的控制，也就是密钥 kk。解密算法类似，使用 128 位的密文和对应的密钥，得到原 128 位的明文

明文可能会很长，也可能会很短，因此块加密需要两个东西

  • padding，即padding到制定分组长度
  • 分组加密模式，即明文分组加密的方式

基本策略

在分组密码设计时，充分使用了 Shannon 提出的两大策略：混淆与扩散两大策略。

混淆

混淆，Confusion，将密文与密钥之间的统计关系变得尽可能复杂，使得攻击者即使获取了密文的一些统计特性，也无法推测密钥。一般使用复杂的非线性变换可以得到很好的混淆效果，常见的方法如下

  • S 盒
  • 乘法

扩散

扩散，Diffusion，使得明文中的每一位影响密文中的许多位。常见的方法有

  • 线性变换
  • 置换
  • 移位，循环移位

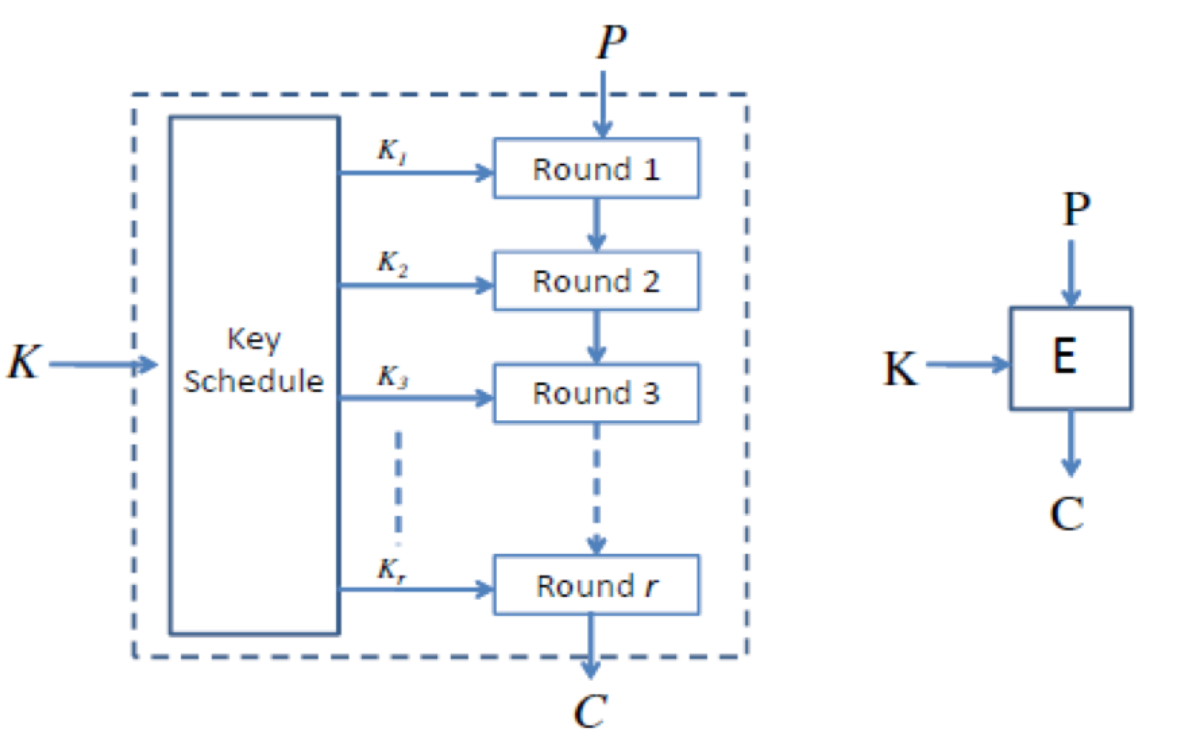
迭代结构

  • 迭代结构

    • 密钥置换
    • 轮加密函数
    • 轮解密函数
image-20240502115119906

  • 轮函数

    Feistel Network，由 Horst Feistel 发明，DES 设计者之一。

    • DES

    Substitution-Permutation Network(SPN)

    • AES

    其他方案

  • 密钥拓展

​ 基本原则是使得密钥的每一个比特尽可能影响多轮的轮密钥。

AES

简介

Advanced Encryption Standard（AES），高级加密标准，是典型的块加密,其基本信息如下

  • 输入：128 比特。
  • 输出：128 比特。
  • SPN 网络结构

SPN网络由节点和边组成，其中节点表示随机变量或者函数，边表示它们之间的依赖关系。SPN具有两种类型的节点：sum节点和product节点。sum节点表示一组随机变量的加权和，而product节点表示一组随机变量的乘积。SPN的计算具有递归结构，从底层的随机变量开始，通过递归地应用sum和product节点来计算整个网络的值。这种结构使得SPN在进行概率推断时能够高效地计算联合概率分布的边缘化和条件概率。

其迭代轮数与密钥长度有关系，如下

密钥长度（比特） 迭代轮数
128 10
192 12
256 14

基本流程

基本概念

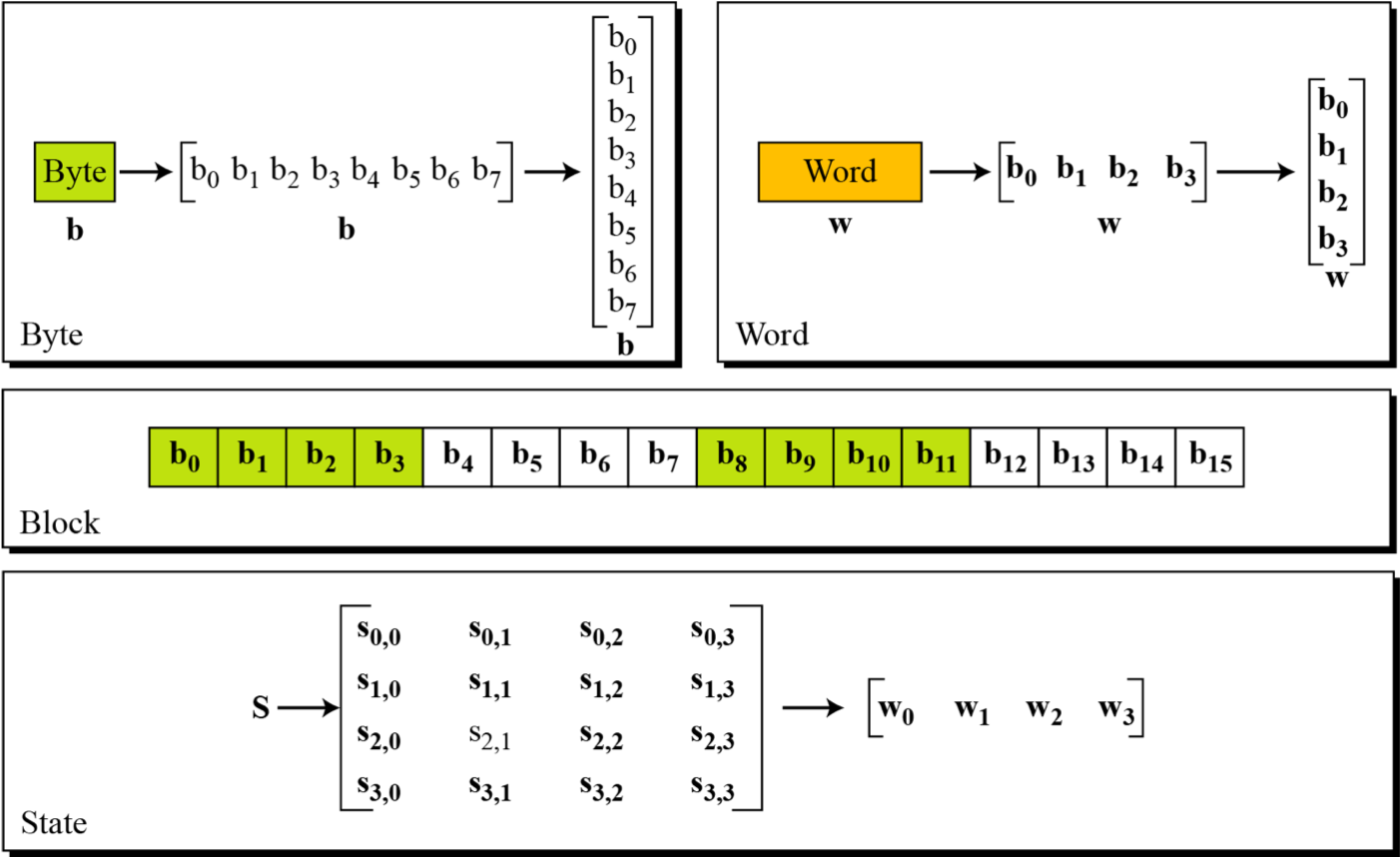
aes_data_unit

在 AES 中，块与 State 之间的转换过程如下

每一个 block 中的字节是按照列排列进入到状态数组的

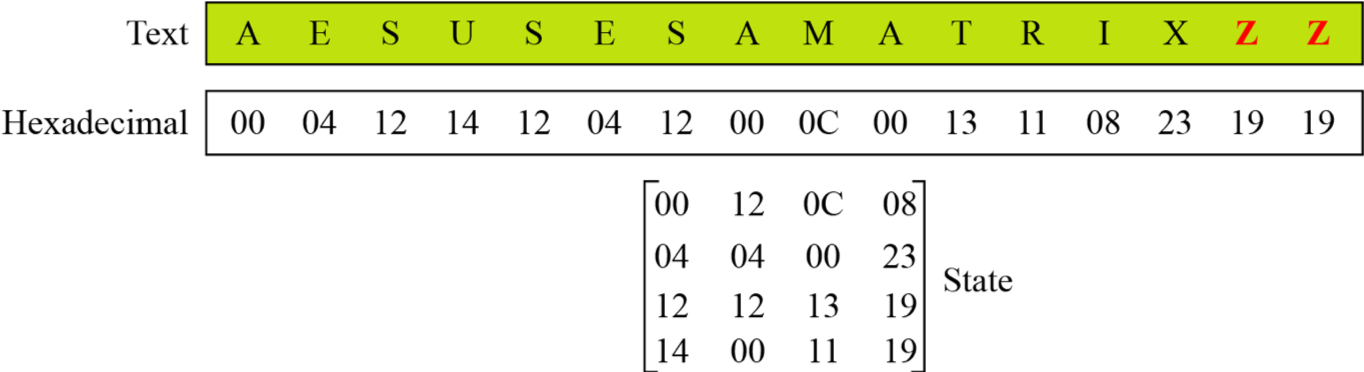
对于明文来说，一般我们会选择使用其十六进制进行编码。

aes_plain2state

加解密流程

总体

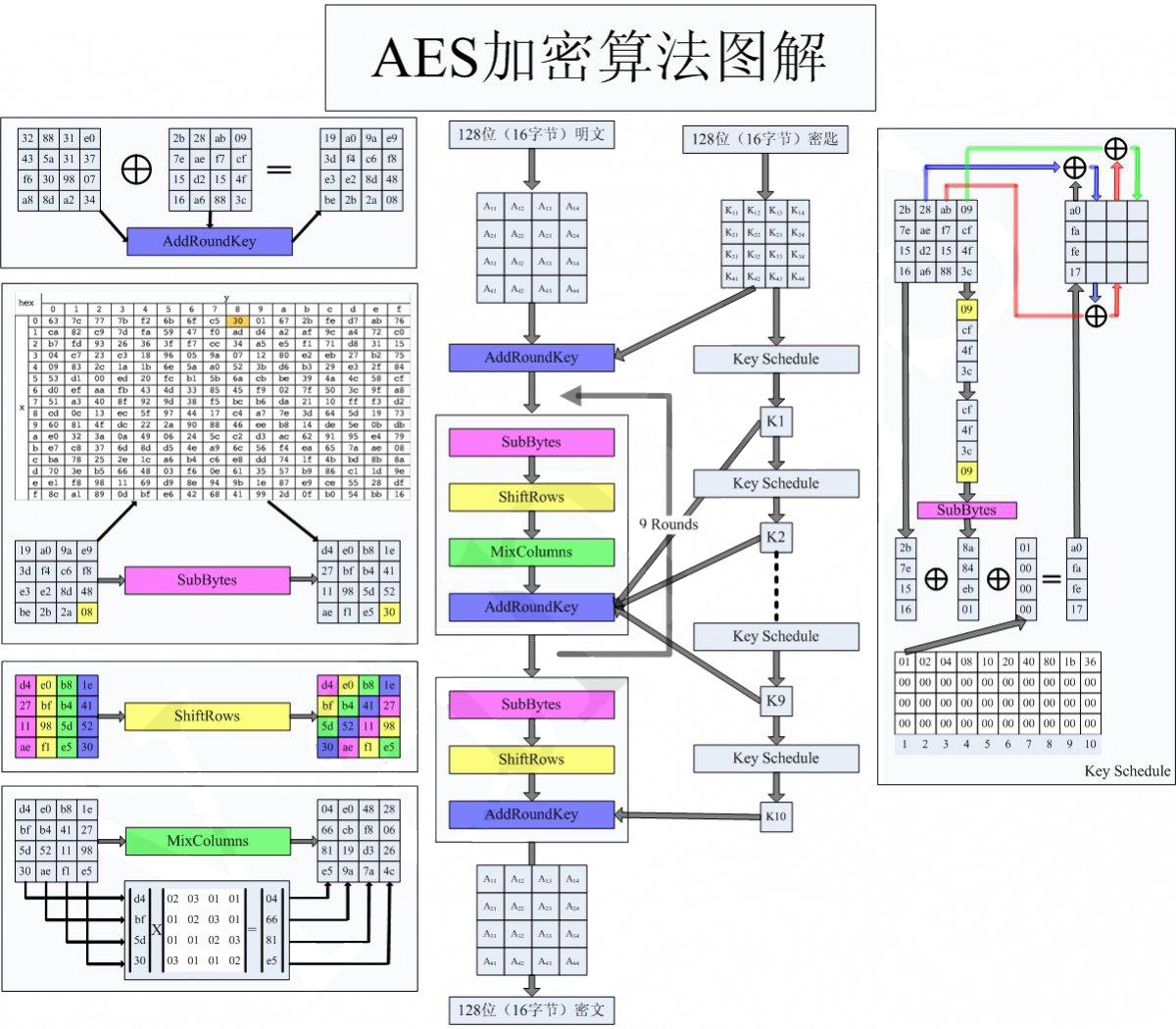aes_detailsAES加密过程是在一个4×4的字节矩阵上运作，这个矩阵又称为“体（state）”，其初值就是一个明文区块（矩阵中一个元素大小就是明文区块中的一个Byte）。（Rijndael加密法因支持更大的区块，其矩阵的“列数（Row number）”可视情况增加）加密时，各轮AES加密循环（除最后一轮外)均包含4个步骤：

  1. AddRoundKey 矩阵中的每一个字节都与该次回合密钥（round key）做XOR运算；每个子密钥由密钥生成方案产生。
  2. SubBytes 透过一个非线性的替换函数，用查找表的方式把每个字节替换成对应的字节。
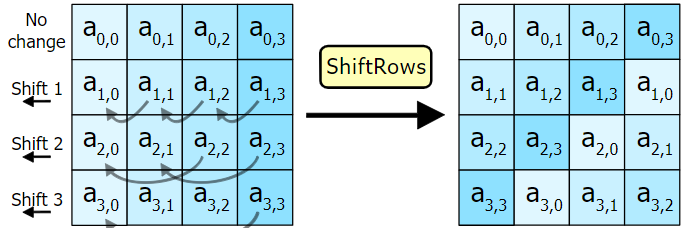
  3. ShiftRows 将矩阵中的每个横列进行循环式移位。
  4. MixColumns 为了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每内联的四个字节。最后一个加密循环中省略MixColumns步骤，而以另一个AddRoundKey取代。

以128bits，迭代10次为例,以下为每一轮所需的操作，我们把第一轮、最后一轮称为“初始轮”、“最终轮”，可以发现，它们只是“中间轮”的简化版：

  • 初始轮（1）
    • AddRoundKey
  • 中间轮（2~9）
    • SubBytes：将数据块中的数据，映射到 Rijndael S-box，主要为了消除特征
    • ShiftRows：将数据块按“行”移位，以达到混淆的目的
    • MixColumns：将数据块按“列”与一个由多项式构成的 matrix，做矩阵乘法。目的是将单个错误扩散到整体，从而达到雪崩效应的预期，使其更难被破解
    • AddRoundKey：将本轮的 key 与数据块相加，由于使用 Galois field，在代码中只是一个简单的 XOR
  • 最终轮（10）
    • SubBytes
    • ShiftRows
    • AddRoundKey

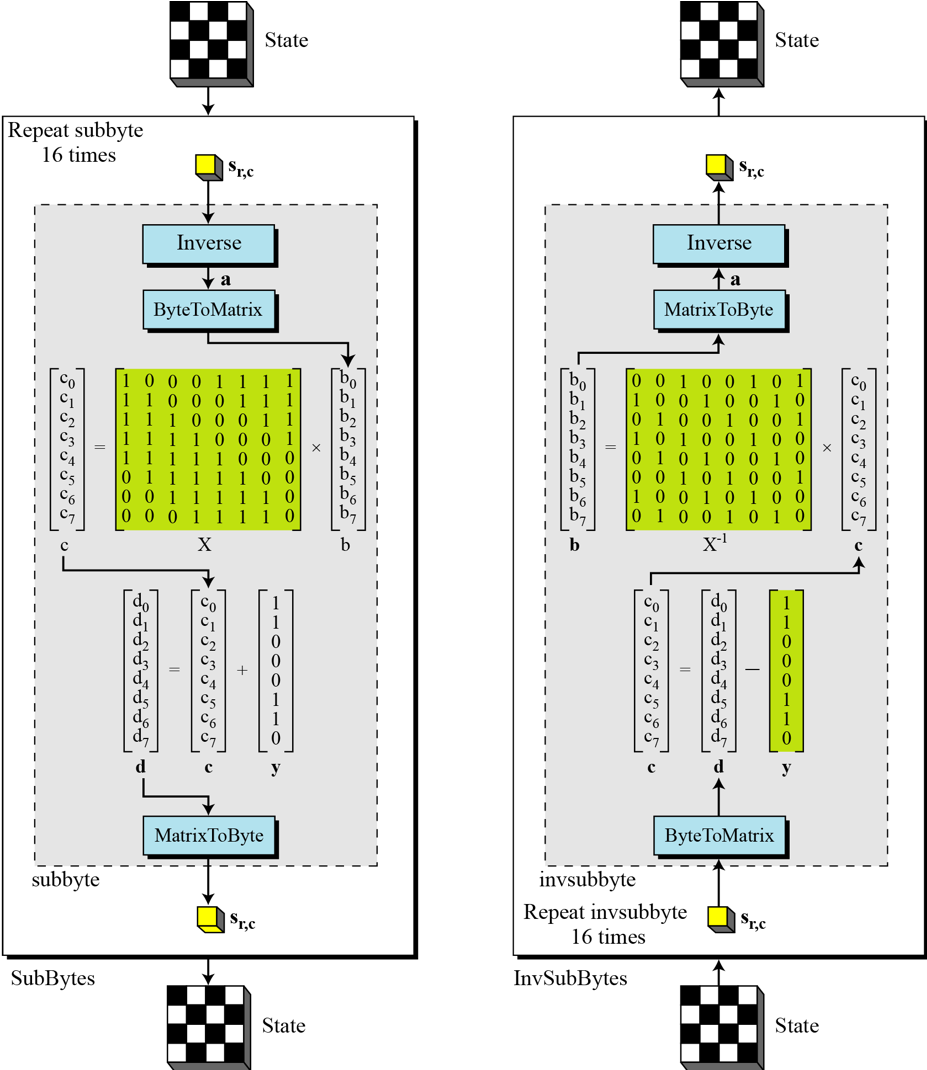
Sbox

SBox
1714634904663

其实s[s7,...,s0]s[s_7,...,s_0]对应sbox的输出

要得出s要经过两个步骤

  • 求出输入 c over GF(28)GF(2^8) 的 GF(2[x]/(x8+x4+x3+x+1)GF(2[x]/(x^8+x^4+x^3+x+1) 乘法逆元
  • 然后将该乘法逆元，与上面的矩阵进行 Affine transformation 运算

Affine transformation 运算即3953

inv_sbox

先求 Affine transformation 运算,在求乘法逆元

在AES中通过Sbox和逆向只用替换映射关系即可

for i in range(256):
    line = (new_s_box[i] & 0xf0) >> 4

    rol = new_s_box[i] & 0xf

    new_contrary_sbox[(line * 16) + rol] = i

字节替换Subbytes

aes_subbytes

列混淆MixColumns

这里的运算是定义在GF(28)GF(2^8)，使用模多项式为x8+x4+x3+1x^8+x^4+x^3+1

密钥扩展

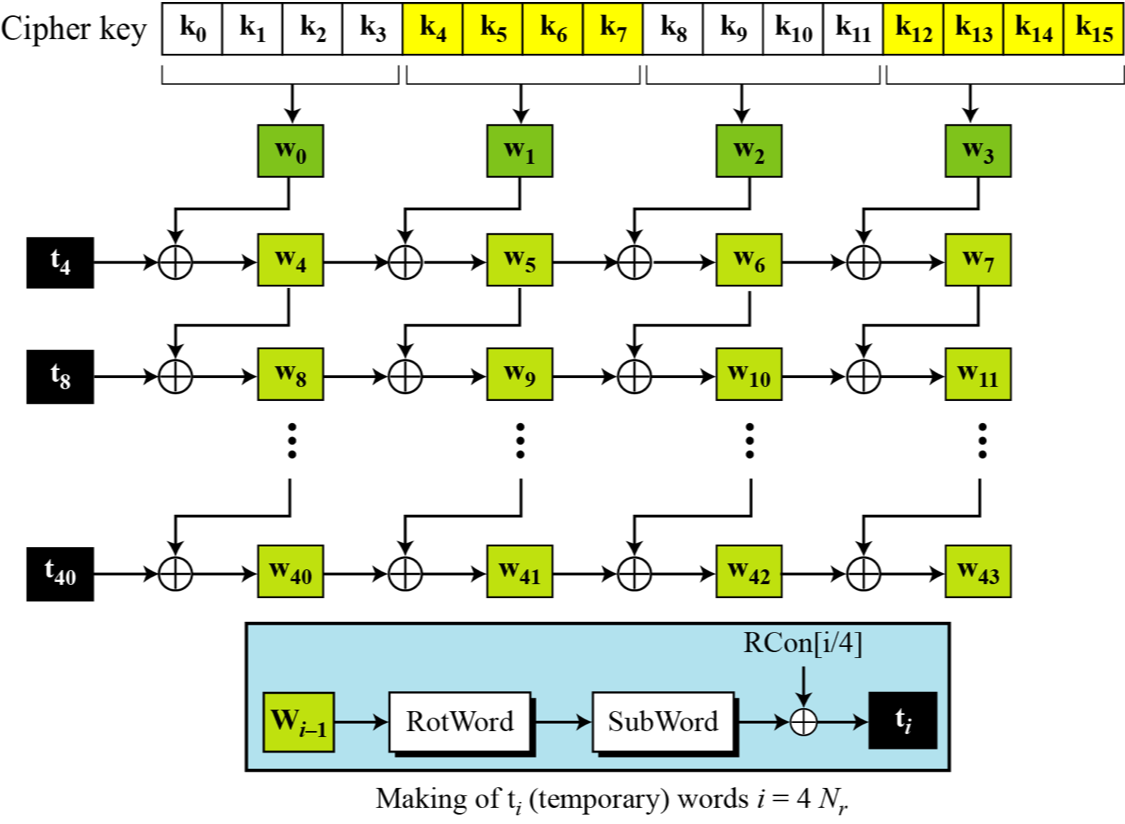
aes_key_expansion

shiftRows

ShiftRows 将数据块按行移位：第 i 行整体向左移动 (i-1) 格。

image-20240502153618109

解密流程

  • 初始轮（10）
    • AddRoundKey
  • 中间轮（9~2）
    • ShiftRows（inverse）
    • SubBytes（inverse）
    • AddRoundKey
    • MixColumns（inverse）
  • 最终轮（1）
    • ShiftRows（inverse）
    • SubBytes（inverse）
    • AddRoundKey

简单实现

s_box = []
s_box_inv = []
rc = [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d]

def sub_bytes(grid, inv=False):
	for i, v in enumerate(grid):
		if inv:  # for decryption
			grid[i] = s_box_inv[v >> 4][v & 0xf]
		else:
			grid[i] = s_box[v >> 4][v & 0xf]

def shift_rows(grid, inv=False):
	for i in range(4):
		if inv:  # for decryption
			grid[i::4] = grid[i::4][-i:] + grid[i::4][:-i]
		else:
			grid[i::4] = grid[i::4][i:] + grid[i::4][:i]

def mix_columns(grid):
	def mul_by_2(n):
		s = (n << 1) & 0xff
		if n & 128:
			s ^= 0x1b
		return s

	def mul_by_3(n):
		return n ^ mul_by_2(n)

	def mix_column(c):
		return [
			mul_by_2(c[0]) ^ mul_by_3(c[1]) ^ c[2] ^ c[3],  # [2 3 1 1]
			c[0] ^ mul_by_2(c[1]) ^ mul_by_3(c[2]) ^ c[3],  # [1 2 3 1]
			c[0] ^ c[1] ^ mul_by_2(c[2]) ^ mul_by_3(c[3]),  # [1 1 2 3]
			mul_by_3(c[0]) ^ c[1] ^ c[2] ^ mul_by_2(c[3]),  # [3 1 1 2]
		]

	for i in range(0, 16, 4):
		grid[i:i + 4] = mix_column(grid[i:i + 4])

def key_expansion(grid):
	for i in range(10 * 4):
		r = grid[-4:]
		if i % 4 == 0:  # 对上一轮最后4字节自循环、S-box置换、轮常数异或，从而计算出当前新一轮最前4字节
			for j, v in enumerate(r[1:] + r[:1]):
				r[j] = s_box[v >> 4][v & 0xf] ^ (rc[i // 4] if j == 0 else 0)

		for j in range(4):
			grid.append(grid[-16] ^ r[j])

	return grid

def add_round_key(grid, round_key):
	for i in range(16):
		grid[i] ^= round_key[i]

def encrypt(b, expanded_key):
	# First round
	add_round_key(b, expanded_key)

	for i in range(1, 10):
		sub_bytes(b)
		shift_rows(b)
		mix_columns(b)
		add_round_key(b, expanded_key[i * 16:])

	# Final round
	sub_bytes(b)
	shift_rows(b)
	add_round_key(b, expanded_key[-16:])
	return b

def decrypt(b, expanded_key):
	# First round
	add_round_key(b, expanded_key[-16:])

	for i in range(9, 0, -1):
		shift_rows(b, True)
		sub_bytes(b, True)
		add_round_key(b, expanded_key[i * 16:])
		for _ in range(3): mix_columns(b)

	# Final round
	shift_rows(b, True)
	sub_bytes(b, True)
	add_round_key(b, expanded_key)
	return b

def aes(typ, key, msg):
	expanded = key_expansion(bytearray(key))

	# Pad the message to a multiple of 16 bytes
	b = bytearray(msg)
	if typ == 0:  # only for encryption
		b = bytearray(msg + b'\x00' * (16 - len(msg) % 16))

	# Encrypt/decrypt the message
	for i in range(0, len(b), 16):
		if typ == 0:
			b[i:i + 16] = encrypt(b[i:i + 16], expanded)
		else:
			b[i:i + 16] = decrypt(b[i:i + 16], expanded)
	return bytes(b)

分组模式